Дополнительные параметры при анализе характеристик во временной области

Схемы, не содержащие реактивных элементов (индуктивностей, емкостей), описываются нелинейными алгебраическими уравнениями.

Если же схема содержит реактивные элементы, то для ее описания потребуются нелинейные интегрально-дифференциальные уравнения. Для их решения используется следующий метод.

Любая схема, может быть представлена в виде двух частей (рис. 4.3), одна из которых содержит линейные и нелинейные безреактивные элементы, а вторая – линейные реактивные компоненты. Модель безреактивной нелинейной части рассмотрена ранее (раздел 4.2). Обратимся теперь к части схемы с реактивными элементами, которая описывается интегрально-дифференциальными уравнениями, зависящими от времени.

Разложим зависимость напряжения на конденсаторе от времени в ряд Тейлора, ограничившись его первыми двумя членами и рассматривая момент времени t-Dt:

,

Тогда справедливо соотношение:

,

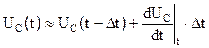при достаточно малом Dt, которое называется шагом интегрирования.

Ток через конденсатор связан с напряжением на нем соотношением

,

подставив которое в разложение, получим

.

Отсюда следует, что напряжение на конденсаторе в момент времени t связано с током через конденсатор законом Ома, причем сопротивление эквивалентного резистора равно 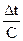, а последовательно с конденсатором включен источник постоянного напряжения, величина которого равна напряжению на конденсаторе в предшествующий момент времени. Таким образом, в любой момент времени конденсатор может быть представлен эквивалентной безреактивной цепью, состоящей из источника постоянного напряжения и резистора.

Аналогичное представление справедливо и для индуктивности, если рассматривать ток через индуктивность:

,

,

;

.

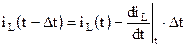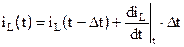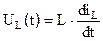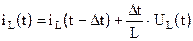Следовательно, индуктивность можно представить в виде параллельного соединения источника постоянного тока, величина которого равна току через индуктивность, протекавшем на предыдущем шаге, и резистора, сопротивление которого равно .

Таким образом, каждый конденсатор и индуктивность в любой момент времени можно заменить эквивалентной схемой (рис. 4.4).

Точность такого представления тем выше, чем меньше шаг интегрирования Dt.

Итак, линейная часть схемы с реактивными компонентами сводится на каждом шаге интегрирования к линейной безреактивной схеме, а вся схема устройства (рис. 4.3) сводится к безреактивной нелинейной схеме, методы анализа которой рассмотрены выше.

Таким образом, второй этап временного анализа нелинейных реактивных схем проводится следующим образом:

Рис. 4.3. Схема с реактивными элементами

Рис. 4.4. Реактивные компоненты и их эквивалентные схемы на каждом шаге итерации

1) Выбирается начальное приближение, то есть начальные токи в ветвях и начальные напряжения в узлах в момент времени t = 0.

2) Задается шаг интегрирования Dt и находится эквивалентная безреактивная схема.

3) Производится расчет режима по постоянному току, т.е. находятся токи в ветвях и напряжения в узлах в момент времени t

4) Полученное для момента времени tрешение принимается за начальное приближение для следующего момента времени t + Dt, и повторяются пункты 2, 3.

5) Решение заканчивается при достижении заданного времени окончания анализа.

Дополнительным параметром является шаг интегрирования Dt, который следует задать при проведении анализа.