Дополнительные параметры при анализе режима по постоянному току

Для того чтобы понять, как задаются дополнительные параметры, рассмотрим основные идеи указанных методов анализа в соответствии с основными этапами моделирования.

Этап составления математического описания схемы устройства выполняется по следующим правилам:

1) Нумеруются все узлы устройства. Один из узлов схемы нумеруется нулевым, то есть базовым, относительно которого отсчитываются узловые напряжения.

2) Для каждого из узлов записывается закон Кирхгофа – сумма токов всех подходящих к узлу ветвей, с учетом принятых направлений токов, равна нулю.

3) Для линейных ветвей их токи выражаются через узловые напряжения.

4) Для нелинейных ветвей записываются дополнительные нелинейные уравнения, связывающие ток через нелинейный элемент с падением напряжения на нем.

Рассмотрим этот этап на примере простейшей схемы (рис. 4.1,а) содержащий один нелинейный элемент – диод Д, включенный последовательно с источником постоянного напряжения Е и резистором R. Будем рассматривать систему узловых напряжений, для чего преобразуем схему к эквивалентному виду (рис. 4.1,б), пронумеруем узлы и зададим направления токов.

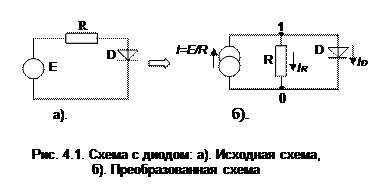Всего узлов один (кроме нулевого). Для него запишем закон Кирхгофа:

.

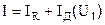Ток линейной ветви I_R выражаем через узловые напряжения, а для тока нелинейной ветви I_R(U₁) записываем уравнение в соответствии с математической моделью диода:

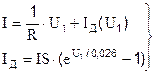
На этом первый этап заканчивается. Аналогично записывается система уравнений сложных схем с большим числом узлов.

Этап решения системы нелинейных уравнений рассмотрим на приведенном выше примере с диодом. Сведем полученную систему к одному нелинейному уравнению:

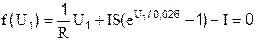
Для того, чтобы найти напряжение на диоде U₁, нужно решить нелинейное уравнение f(U₁)=0, то есть найти корень уравнения U1⁽*⁾, при котором функция f(U1⁽*⁾) равна нулю.

Решение уравнения осуществляется методом Ньютона-Рафсона, суть которого проиллюстрируем следующим образом.

Пусть график функции f(U1) имеет вид, представленный на рис. 4.2,а.

Возьмем произвольную точку нулевого приближения U1⁽⁰⁾ и восстановим перпендикуляр до пересечения с графиком функции. Из точки пересечения проведем касательную к кривой до пересечения с осью U1в точке U1⁽¹⁾, которая расположена ближе к точке решения U1^(*), чем точка нулевого приближения U1⁽⁰⁾. Повторяя этот процесс, найдем последовательность точек U1⁽⁰⁾, U1⁽¹⁾, U1⁽²⁾,… U1⁽ⁿ⁾, U1⁽ⁿ⁺¹⁾…, которая приближается (сходится) к искомой точке решения U1^(*).

Такой пошаговый итеративный процесс отыскания решения уравнения математически записывается следующим образом.

Пусть на шаге с номером n найдено значение напряжения U₁⁽ⁿ⁾ и соответствующее ему значение функции f(U1⁽ⁿ⁾). Разложим функцию f(U1) в ряд Тейлора в окрестностях точки U1⁽ⁿ⁾, ограничившись первыми двумя членами ряда, и прировняем ее к нулю:

,

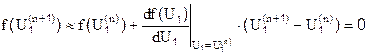где 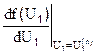есть производная от функции f(U1) , вычисленная в точке U1⁽ⁿ⁾.

Решая это уравнение, найдем следующую (n+1) точку, то есть сделаем (n+1)-й шаг итерации:

.

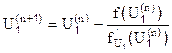Далее, повторяя вычисления по последней формуле, получим все последующие точки последовательности. Так как сама функция задана в виде

,

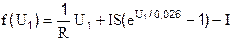то производная от нее находится простым дифференцированием:

,

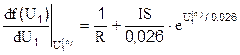Для отыскивания точного решения U₁^(*) итерационный процесс должен быть бесконечным. Реально нас интересует не абсолютно точное решение U1^(*), а приближенное, определяемое с заданной инженерной точностью. При достижении этой точности процесс может быть остановлен, полученное решение принимается за точное. Это делается заданием точности решения либо числа шагов итерации, которые и являются дополнительными параметрами; их нужно задавать при проведении статического и временного анализа в рассматриваемом пакете программ.

Существует еще один дополнительный параметр, необходимость введения которого вызвана следующими обстоятельствами.

Доказано, что для сходимости итераций к искомой точке необходимо, чтобы угол наклона касательных был достаточно велик, в противном случае процесс расходится от точки решения, и решение задачи анализа дает сбой.

Проиллюстрируем это на рис. 4.2,б. Здесь точки U1⁽¹⁾, U1⁽²⁾ не приближаются к искомой точке U1^(*),а удаляются (расходятся), что определяется видом функции f(U1) и выбором точки начального приближения U1⁽⁰⁾.

При проведении анализа мы имеем дела только с принципиальной схемой и не знаем ни вида функции, ни способа выбора начального приближения. Поэтому для некоторых схем при неудачном выборе начального приближения U1⁽⁰⁾ происходит сбой в процессе анализа.

Начальные напряжения U1⁽⁰⁾ в узлах схемы также являются дополнительными параметрами. Опыт эксплуатации данного пакета программ показывает, что для большинства схем можно выбрать U1⁽⁰⁾=0, то есть начальные приближения должны быть нулевыми (zero).