Понятие о шумовых характеристиках

Сигнал на выходе РЭС содержит как полезную составляющую, так и помехи. Помехи могут быть детерминированными и случайными. В последнем случае они называются шумами. Мы будем рассматривать шумы, создаваемые самим РЭС. В этом случае источниками шумов являются радиокомпоненты РЭС.

Важным параметром источника шума является спектральная плотность мощности, то есть мощность случайного сигнала, отнесённая к полосе частот в 1 Гц.

Введём некоторые определения. Пусть сигнал U(t) задан на всём отрезке времени, но, в отличие от рассмотренного в предыдущем разделе, не является периодическим. Тогда при определённых условиях, которые мы здесь не рассматриваем, он может быть представлен в виде интеграла Фурье

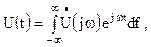
где 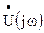- комплексная спектральная плотность периодического сигнала. Величина 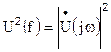называется спектральной плотностью мощности (СПМ), то есть равна мощности сигнала на частоте f, выделяемого на сопротивлении 1 Ом, отнесённой к полосе частот 1 Гц

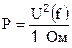
Так как шум является случайным процессом, то СПМ шума находится усреднением величины U²(f) на множестве реализаций случайного процесса и записывается в виде 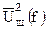, где индекс “ш” указывает, что в качестве сигнала рассматривается шум, а черта сверху означает операцию усреднения.

В общем случае СПМ шума зависит от частоты. Шум, у которого этой зависимости нет, то есть выполняется условие , называется белым шумом.

Шумы в РЭС возникают за счёт тепловых шумов резисторов и дробовых шумов других компонентов (транзисторов, диодов, ламп, операционных усилителей и т.д.).

Шум, создаваемый резистором с сопротивлением R, является белым, так как его СПМ не зависит от частоты и определяется формулой Найквиста 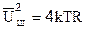, где k -постоянная Больцмана, Т - абсолютная температура. Таким образом, резистор является источником напряжения шума со спектральной плотностью среднеквадратического напряжения (СПН), равной 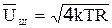. Шумовая модель резистора изображена на рис 3.2:

Шумовые модели других компонентов включают в себя один или несколько источников шума, спектральные плотности среднеквадратических напряжений которых в общем случае не зависят от частоты. В настоящее время все шумовые модели компонентов РЭС разработаны и включены в библиотеку моделей в системах моделирования.

Таким образом, РЭС при анализе шумов представляет собой линейную модель схемы, к различным точкам которой подключены источники шума с напряжением, равным спектральной плотности среднеквадратического напряжения шума 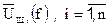, где n - число источников. Так как СПМ шума 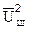имеет размерность В²/Гц, то СПН шума 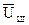имеет размерность .

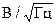На рис 3.3 условно изображена шумовая модель РЭС, включая сопротивления источника сигнала R₁ и нагрузки R_Н .

Здесь , …, 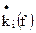- комплексные коэффициенты передачи от соответствующих источников шума к выходу. Так как все источники шума статистически независимы, то суммарная СПМ шума на выходе (U_швых)² равна сумме вкладов СПМ шума от каждого из источников:

Отсюда СПН шума на выходе 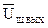находится по формуле

,

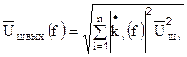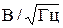
В системах моделирования Microcap величина является результатом расчёта шума.

При проектировании РЭС интерес представляет не спектральная плотность мощности шума, а сама мощность шума в диапазоне частот [f₁, f₂] либо в этом же диапазоне напряжение шума 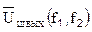. Искомые величины находятся по формулам

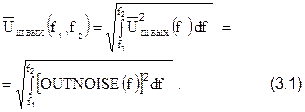
Рассмотрим отношение СПМ сигнала 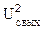на выходе к СПМ шума на выходе 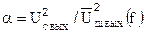. Поделим числитель и знаменатель этого отношения на квадрат модуля коэффициента передачи от входа РЭС к выходу :

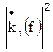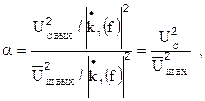
где U_с - напряжение сигнала на входе, 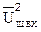- приведённая ко входу СПМ шума.

В системе MicroCap 7 результатом расчёта кроме величины OUTNOISE является величина INNOISE (f):

,

равная СПН шума, приведенной ко входу.

Из полученных соотношений можно найти отношение сигнал/шум проектируемого РЭС в диапазоне частот [f₁, f₂] :

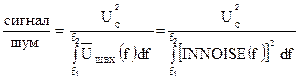(3.2)

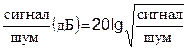(3.3)

Язык системы MicroCap 7 обеспечивает возможность прямого расчёта по формулам (3.1), (3.2).