Передача тепла теплопроводностью
Уравнение теплопроводности для установившегося теплового потока через однослойную плоскую стенку:
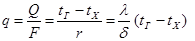 (2.1)
(2.1)
где q – удельный тепловой поток (удельная тепловая нагрузка), Вт/м2; Q – тепловой поток (расход теплоты), Вт; F – площадь поверхности стенки, м2; tГ и tХ – температуры горячей и холодной поверхности стенки, оС; r = δ/λ – термическое сопротивление стенки, (м2∙К)/Вт; δ – толщина стенки, м; λ – коэффициент теплопроводности, Вт/(м∙К).
Уравнение теплопроводности для установившегося теплового потока через многослойную плоскую стенку:
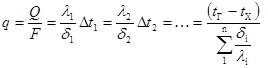 (2.2)
(2.2)
Для цилиндрической однослойной стенки средняя площадь поверхности определяется по формуле:
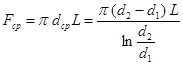 (2.3)
(2.3)
где d1 и d2 – внутренний и наружный диаметры; L – длина цилиндра, м.
Уравнение теплопроводности для установившегося теплового потока через однослойную цилиндрическую стенку:
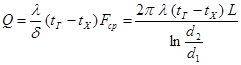 (2.4)
(2.4)
Здесь δ = (d2 – d1) / 2.
Если d2 / d1 < 2, то вместо вычисления по формуле (2.3) можно с достаточной точностью принимать для средней площади поверхности однослойной цилиндрической стенки величину
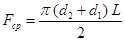 (2.5)
(2.5)
Уравнение теплопроводности для установившегося теплового потока через многослойную цилиндрическую стенку:
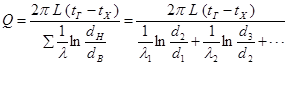 (2.6)
(2.6)
Здесь dВ и dН – внутренний и наружный диаметры каждого цилиндрического слоя.
При отсутствии экспериментальных данных коэффициент теплопроводности жидкости λ [в Вт/(м∙К)] при температуре ~ 30оС может быть рассчитан по формуле:
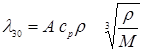 (2.7)
(2.7)
где ср – удельная теплоемкость жидкости, Дж/(кг∙К); ρ – плотность жидкости, кг/м3; М – мольная масса жидкости, кг/кмоль; А – коэффициент, зависящий от степени ассоциации жидкости. Для ассоциированных (например, воды) А = 3,58∙10-3, для неассоциированных (например, бензола) А = 4,22∙10-8.
Либо коэффициент теплопроводности жидкости находят по следующему уравнению:
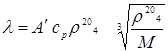 (2.8)
(2.8)
где ср – удельная теплоемкость жидкости, Дж/(кг∙К); 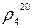 – относительная плотность жидкости (по отношению к воде); М – мольная масса жидкости, кг/кмоль; А' – коэффициент, зависящий от степени ассоциации жидкости. Для ассоциированных А' = 1,29, для неассоциированных А' = 1,52.
– относительная плотность жидкости (по отношению к воде); М – мольная масса жидкости, кг/кмоль; А' – коэффициент, зависящий от степени ассоциации жидкости. Для ассоциированных А' = 1,29, для неассоциированных А' = 1,52.
Коэффициент теплопроводности жидкости при температуре t определяется по формуле:
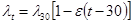 (2.9)
(2.9)
где ε – температурный коэффициент. Значения ε·103:
| Анилин | 1,4 | Метиловый спирт | 1,2 | Хлорбензол | 1,5 |
| Ацетон | 2,2 | Нитробензол | 1,0 | Хлороформ | 1,8 |
| Бензол | 1,8 | Пропиловый спирт | 1,4 | Этилацетат | 2,1 |
| Гексан | 2,0 | Уксусная кислота | 1,2 | Этиловый спирт | 1,4 |
Коэффициент теплопроводности водного раствора при температуре t определяется по формуле:
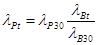 (2.10)
(2.10)
где λр и λв – коэффициенты теплопроводности раствора и воды.
Коэффициент теплопроводности газа при невысоких давлениях может быть вычислен по формуле:
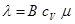 (2.11)
(2.11)
где μ – динамический коэффициент вязкости газа, Па·с; В=(9k - 5)/4; k = cP/cV – показатели адиабаты; cP и cV - удельная теплоемкость газа при постоянном давлении и при постоянном объеме, соответственно, Дж/(кг·К).
Для одноатомных газов В = 2,5, для двухатомных В = 1,9, для трехатомных В = 1,72.
Теплопроводность смесей газов можно определить с помощью приближенного уравнения
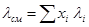 (2.12)
(2.12)
где xi – мольная доля i-го компонента; λi – теплопроводность i-го компонента.
Теплоотдача
Теплоотдачей называется стадия теплопереноса через пограничную пленку.
Конвективный поток тепла выражается уравнением
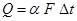 (2.13)
(2.13)
где Q – количество тепла, передаваемое в единицу времени, Вт; F – поверхность теплообмена, м2; Dt – разность между температурой массы жидкости и температурой теплоотдающей (тепловоспринимающей) поверхности, К; α – коэффициент теплоотдачи, Вт/(м2·К).
Выбор уравнений для уточненного расчета коэффициентов теплоотдачи зависит от характера теплообмена (без изменения агрегатного состояния, при кипении или при конденсации), от вида выбранной поверхности теплообмена (плоской, гофрированной, трубчатой, оребренной), от типа конструкции (кожухотрубчатые, двухтрубные, змеевиковые и др.), от режима движения теплоносителя. В общем виде критериальная зависимость для определения коэффициентов теплоотдачи имеет вид:
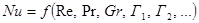 (2.14)
(2.14)
Здесь Г1, Г2,... – симплексы геометрического подобия.
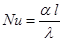 - критерий Нуссельта,
- критерий Нуссельта,
где α – коэффициент теплоотдачи, Вт/(м2·оС); λ – коэффициент теплопроводности, Вт/оС; l – линейный размер, определяющий процесс теплопередачи, м;
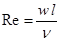 - критерий Рейнольдса,
- критерий Рейнольдса,
где w – скорость среды, м/сек; n - кинематическая вязкость среды, м2/сек; l – линейный размер, определяющий режим движения среды, м;
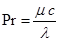 - критерий Прандтля,
- критерий Прандтля,
где μ – динамическая вязкость жидкости ( 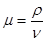 ), Н·сек/м2; ср – удельная теплоемкость жидкости, Дж/(кг·оС);
), Н·сек/м2; ср – удельная теплоемкость жидкости, Дж/(кг·оС);
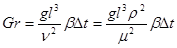 - критерий Грасгофа,
- критерий Грасгофа,
где β – коэффициент объемного расширения, К-1; Dt – разность температур стенки и жидкости, К.
Коэффициент теплоотдачи находится по уравнению
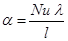
Во многие критериальные уравнения входит множитель (Pr/Prст)0,25,учитывающий направление теплового потока. Для газов Pr/Prст = 1 как при нагревании, так и при охлаждении.
Необходимо помнить, что при расчете Pr свойства определяются при температуре жидкости, а для Prст – при температуре стенки.
Приближенные значения критерия Pr для газов, рекомендуемые для расчетов:
Одноатомные газы 0,67
Двухатомные газы 0,72
Трехатомные газы 0,8
Четырех- и многоатомные газы 1,0
В некоторые расчетные формулы для определения коэффициента теплоотдачи в явном или неявном виде входит температура стенки. Ее можно определить из соотношения
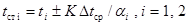 (2.15)
(2.15)
В табл. 2.1 приведены уравнения для расчета коэффициентов теплоотдачи в наиболее часто встречающихся случаях теплообмена.
В формулах встречается понятие эквивалентного диаметра трубы - 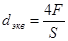 , где F – площадь поперечного сечения трубы, м2; S – полный периметр поперечного сечения потока, независимо от того, какая часть этого периметра участвует в теплообмене, м.
, где F – площадь поперечного сечения трубы, м2; S – полный периметр поперечного сечения потока, независимо от того, какая часть этого периметра участвует в теплообмене, м.
Таблица 2.1.
Дата добавления: 2020-10-25; просмотров: 906;











