Стационарная теплопроводность плоской, однородной, изотропной, бесконечной стенки без внутренних источников теплоты при граничных условиях первого рода.

Запишем уравнение Фурье-Кирхгофа:
 |
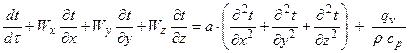
 |
Целью решения является:
Определение закона изменения температуры в теле;
Определение величины теплового потока.
Решается задача путем интегрирования дифференциального уравне-ния [1]:
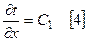
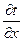 - температурный градиент этого объекта.
- температурный градиент этого объекта.
Разделяем переменные и интегрируем [2]:
Получаем:
t = C1x+C2 [5] – общее решение задачи.
Температура изменяется линейно.
Частное решение определяется при определении С1 и С2.
При условии [2] tc1 = C2 [6];
При условии [3] tc2 = C1 d + tc1 ;
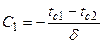 [7];
[7];
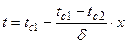 [8] – частное решение.
[8] – частное решение.
Подставляя x можно определить любую температуру.
Вторая часть задачи решается по закону Фурье.
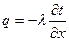 подставляем в [7];
подставляем в [7];
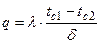 [9] – уравнение плотности теплового потока.
[9] – уравнение плотности теплового потока.

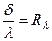 - термическое сопротивление стенки.
- термическое сопротивление стенки.
Таким образом, плотность теплового потока при теплопроводности прямопропорциональна температурному напору и обратнопропорциональна термическому сопротивлению.
Если необходимо определить полный тепловой поток, то:
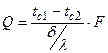 [10].
[10].
Дата добавления: 2018-11-26; просмотров: 1031;











