Стационарная случайная функция и свойства ее характеристик.
На практике встречаются процессы, которые имеют вид непрерывных случайных колебаний относительно некоторого среднего значения. При этом средняя амплитуда и характер этих колебаний с течением времени существенно не изменяется; их реализации имеют примерно одинаковый характер. Такие процессы относят к стационарным случайным процессам.
Случайный процесс называют стационарным, если n-мерная плотность вероятности не меняется при любом сдвиге 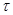 всей группы точек
всей группы точек 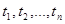 вдоль оси времени, т.е.
вдоль оси времени, т.е.
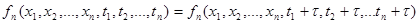 . (6.10)
. (6.10)
Примерами таких процессов являются: шумы в приемнике после его включения; шумы ламп, полупроводниковых приборов, резисторов, колебания самолета на установившемся режиме полета, случайные ошибки автоматических систем относятся к стационарным случайным процессам (рис. 6.7).
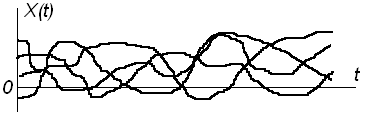
Рисунок 6.7 – Реализации стационарного случайного процесса
К нестационарным случайным процессам обычно относят, например, шумы приемника при его включении, модулированные по амплитуде и частоте шумовые колебания, потребление электроэнергии в городе в течение суток и другие не установившиеся случайные процессы (рис. 6.8).
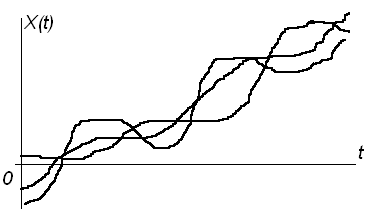
Рисунок 6.8 – Нестационарные случайные процессы
Случайный процесс X(t), у которого вероятностные характеристики при любом 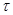 совпадают с соответствующими характеристиками случайного процесса
совпадают с соответствующими характеристиками случайного процесса 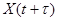 , называют стационарным в узком (строгом) смысле.
, называют стационарным в узком (строгом) смысле.
Случайный процесс X(t) называют стационарным, если математическое ожидание является постоянным, а корреляционная функция зависит только от разности 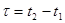 аргументов, т.е.
аргументов, т.е. 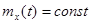 , а
, а 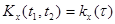 . Такой случайный процесс является стационарным в широком смысле.
. Такой случайный процесс является стационарным в широком смысле.
Из определения стационарности процесса вытекает, что среднее значение во всех сечениях процесса остается постоянным и не зависит от времени. Это значит, что оно является характеристикой не отдельных сечений, а процесса в целом. При этом математическое ожидание характеризует положение реализаций относительно оси абсцисс. Если оно равно нулю, то это означает, что отклонения в положительную и в отрицательную сторону в среднем одинаковы.
Корреляционная функция стационарного случайного процесса характеризуется следующими основными свойствами.
1 Дисперсия стационарного случайного процесса постоянна и равна значению корреляционной функции в начале координат, т.е.
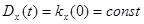 .
.
2 Корреляционная функция стационарного случайного процесса является четной, т.е.
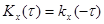 .
.
График корреляционной функции 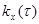 геометрически представляет собой симметричную относительно оси ординат кривую. Часто в различных приложениях встречается показательная корреляционная функция (рис. 6.9).
геометрически представляет собой симметричную относительно оси ординат кривую. Часто в различных приложениях встречается показательная корреляционная функция (рис. 6.9).
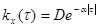 .
.
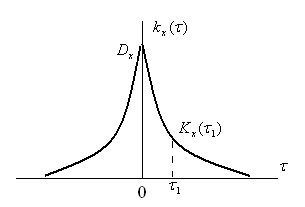
Рисунок 6.9 – График показательной корреляционной функции
Нормированная корреляционная функция стационарного случайного процесса 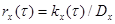 , представляет собой коэффициент корреляции, зависящий только от величины
, представляет собой коэффициент корреляции, зависящий только от величины 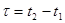 .
.
Случайный процесс называется эргодическим, если любая ее реализация несет в себе всю информацию о случайном процессе.
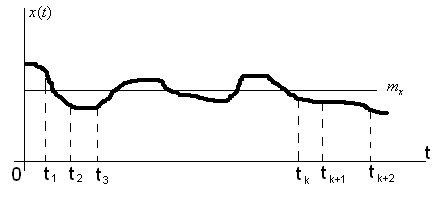
Рисунок 6.10 – Реализация стационарного случайного процесса
Эргодическое свойство имеют те стационарные случайные функции, которые не содержат в своем составе обыкновенную случайную величину.
Если стационарная случайная функция X(t) обладает эргодическим свойством, то:
а) ее математическое ожидание 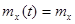 приближенно равно средней по времени ординате одной произвольно взятой реализации
приближенно равно средней по времени ординате одной произвольно взятой реализации 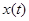 достаточно большой продолжительности (рис. 6.10):
достаточно большой продолжительности (рис. 6.10):
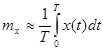 ; (6.11)
; (6.11)
б) значение корреляционной функции 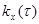 при любом значении
при любом значении 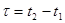 приближенно равно произведению отклонения одной реализации
приближенно равно произведению отклонения одной реализации 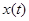 в точках, отстоящих друг от друга на величину
в точках, отстоящих друг от друга на величину 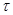 , от математического ожидания
, от математического ожидания 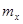 стационарной случайной функции
стационарной случайной функции
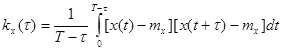 . (6.12)
. (6.12)
Если 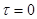 , то
, то 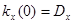 и
и
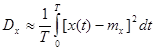 .
.
Дата добавления: 2021-11-16; просмотров: 608;











