Одноканальная система с отказами.
Рассмотрим задачу. Имеется один канал, на который поступает поток заявок с интенсивностью l. Поток обслуживании имеет интенсивность m. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет два состояния: S0 — канал свободен, S1 — канал занят. Размеченный граф состояний представлен на рис. 3.4.
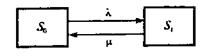
Рис. 3.4
Здесь и в дальнейшем предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. К ним относится и поток обслуживании — поток заявок, обслуживаемых одним непрерывно занятым каналом. Среднее время обслуживания tоб обратно по величине интенсивности 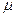 , т.е.
, т.е. 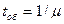 .
.
В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид
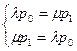
т.е. система вырождается в одно уравнение. Учитывая нормировочное условие р0 + p1 = l, найдем из (15.18) предельные вероятности состояний
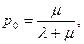
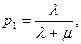
которые выражают среднее относительное время пребывания системы в состоянии S0 (когда канал свободен) и S1 (когда канал занят), т.е. определяют соответственно относительную пропускную способность Q системы и вероятность отказа ротк.
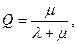
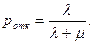
Абсолютную пропускную способность найдем, умножив относительную пропускную способность Q на интенсивность потока отказов
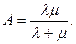
Дата добавления: 2016-11-26; просмотров: 1589;











