Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 3.2.

Рис. 3.2

Рассмотрим упорядоченное множество состояний системы S₀, S₁, S₂, ..., S_k. Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния S_k возможны переходы только либо в состояние S_k-1, либо в состояние S_k+1.

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивноcтями 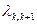или .

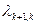По графу, представленному на рис. 15, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений получим: для состояния S_n

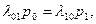
которое с учетом

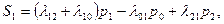
для состояния (15.12) приводится к виду

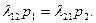
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

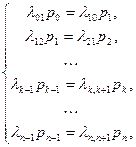(3.6)

к которой добавляется нормировочное условие

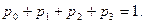(3.7)

При анализе численности популяций считают, что состояние S_k соответствует численности популяции, равной k, и переход системы из состояния S_k в состояние S_k+1 происходит при рождении одного члена популяции, а переход в состояние S_k-1 — при гибели одного члена популяции.

Решая систему (3.6), (3.7), можно получить

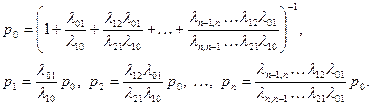(3.8)

Пример 02

В условиях задачи 15.5 определить оптимальное число телефонных номеров в телевизионном ателье, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 90 заявок на переговоры.

Решение. Интенсивность нагрузки канала по формуле (15.25) 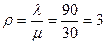, т.е. за время среднего (по продолжительности) телефонного разговора мин. поступает в среднем 3 заявки на переговори.

Будем постепенно увеличивать число каналов (телефонньїх номеров) п = 2, З, 4, ... й определим по формулам (15.25), (15.28), (15.29) для получаемой п - канальной СМО характеристики обслуживания.

При п = 2

.

.

.

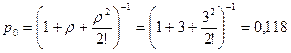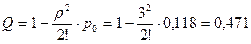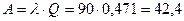При п = 3

.

.

.

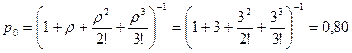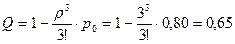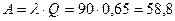При п = 4

.

.

.

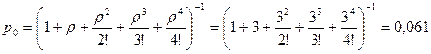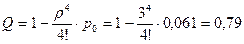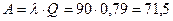При п = 5

.

.

.

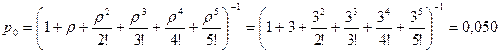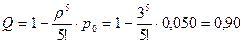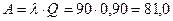При п = 5

.

.

.

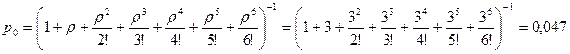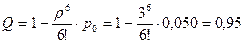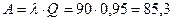Значение характеристик СМО сведем в табл. 15.1. *

Таблица 15.1

Характеристика обслужи­вания	Число каналов (телефонных номеров)
Относительная пропу­скная способность	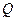0,25	0,47	0,65	0,79	0,90	0,95
Абсолютная пропускная способность А	22,5	42,4	58,8	71,5	81,0	85,3

По условию оптимальности ( 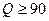, следовательно, в телевизионном ате­лье необходимо установить 5 телефонных номеров (в этом случае 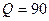— см. табл. 15.1). При этом в час будут обслуживаться в среднем 81 заявок (А = 81), а среднее число занятых телефонных номеров (каналов) по формуле (15.30)

.

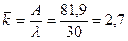СМО с отказами

В качестве показателей эффективности СМО с отказами будем рассматривать:

А — абсолютную пропускную способность СМО, т.е. среднее

число заявок, обслуживаемых в единицу времени;

Q — относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

р_отк. ^— вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

k — среднее число занятых каналов (для многоканальной системы).