Аналитический способ сложения сходящейся системы сил
Для аналитического задания силы необходимо выбрать систему координационных осей, по отношению к которым будет определяться направление силы в пространстве.
Вектор, изображающий силу, можно построить, если известны её проекции на прямоугольные декартовы оси координат.
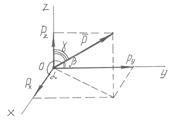
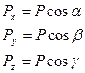
Сила 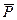 разложена на составляющие
разложена на составляющие 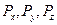 , которые численно равны проекциям силы на соответствующие оси. Отсюда следует, что если известны проекции силы на оси координат, то можно вектор силы построить геометрически.
, которые численно равны проекциям силы на соответствующие оси. Отсюда следует, что если известны проекции силы на оси координат, то можно вектор силы построить геометрически.
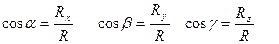
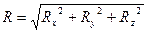 ,
,
где 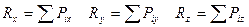
Чтобы сложить силы аналитически, необходимо вычислить проекции сил на координатные оси.
Аналитическое условие равновесия сходящейся системы сил.
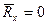 , т.е. и
, т.е. и 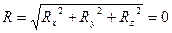 , тогда
, тогда
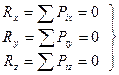
-аналитическое выражение равновесия пространственной сходящейся системы сил.
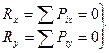 - для плоской системы сил
- для плоской системы сил
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три взаимноперпендикулярных оси были равны 0.
Лекция 3.
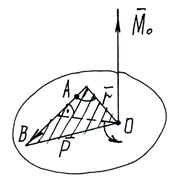 Момент силы относительно точки.
Момент силы относительно точки.
Дано: тело с неподвижной т.О, в т.А приложена сила 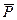 , которая стремится повернуть тело вокруг т.О. Такое действие силы называется вращательным эффектом. Вращательный эффект изменяется моментом силы относительно точки:
, которая стремится повернуть тело вокруг т.О. Такое действие силы называется вращательным эффектом. Вращательный эффект изменяется моментом силы относительно точки: 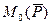 .
.
Момент силы 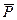 относительно т.О изображается вектором
относительно т.О изображается вектором 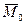 приложенным в этой точке и направленным перпендикулярно к плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу
приложенным в этой точке и направленным перпендикулярно к плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу 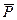 , стремящуюся вращать эту плоскость в сторону, обратную вращению часовой стрелки.
, стремящуюся вращать эту плоскость в сторону, обратную вращению часовой стрелки.
Модуль этого вектора: 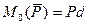 ,
,
где d – плечо - кратчайшее расстояние от т.О до линии действия силы.
Модуль можно выразить 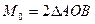
Момент силы равен, нулю если d=0
Если в т.А провести 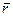 , то
, то 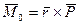
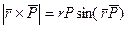 , но
, но 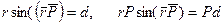
Вектор момента силы 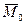 относительно т.О можно рассматривать как векторное произведение
относительно т.О можно рассматривать как векторное произведение 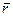 , проведенного из этой точки в точку приложения силы на вектор силы
, проведенного из этой точки в точку приложения силы на вектор силы 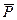 .
.
Дата добавления: 2016-06-29; просмотров: 5432;











