Отображения и функционалы

Наиболее общий способ установления отношения между элементами состоит в отображении элементов одного множества на элементы другого.

Отображение – это правило, в соответствии с которым элементу одного множества, скажем 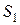, ставится в соответствие элемент другого множества, скажем 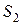. Символически отображение обозначается как 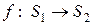, что является компактной формой следующего выражения:

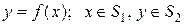. (1.1.8)

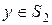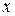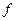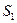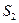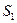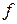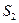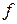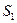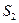Элемент называется образом элемента при отображении . Множество является областью определения отображения, а входящее в множество всех образов элементов из является областью изображений. Если область изображений совпадает с , то говорят, что есть отображение на . Отображение всегда однозначно в том смысле, что для каждого элемента 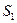существует только один образ (по определению). Если различным элементам из 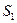соответствуют различные изображения в 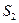, то отображение взаимно-однозначное.

Пусть, например, 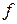есть отображение вида

.

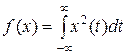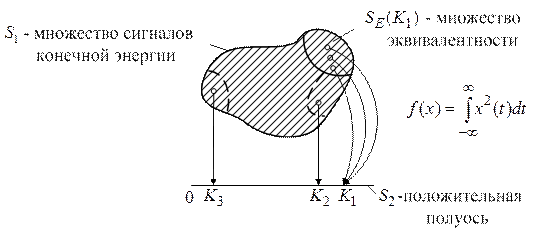
Тогда мы имеем отображение множества сигналов на действительную положительную полуось в соответствии с их энергией, как показано на рис. 1.3. В этом случае отношение эквивалентности, соответствующее 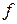, разбивает 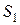на подмножества сигналов с равной энергией.

то преобразование Фурье 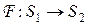есть отображение в другое множество функций с интегрируемым квадратом

.

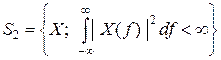Отображение задается следующим образом:

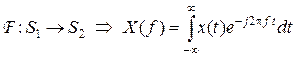. (1.1.9)

Преобразование Фурьеявляется отображением, широко используемым в теории сигналов. Если 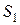- множество сигналов с ограниченной энергией

,

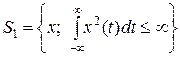то преобразование Фурье 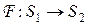есть отображение в другое множество функций с интегрируемым квадратом

.

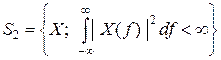Отображение задается следующим образом:

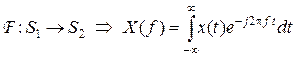. (1.1.9)

Если подходить строго, то это отображение не взаимно-однозначное, т.к. может существовать две и более функций времени, таких, как показано на рис. 1.4., для которых преобразование Фурье одинаково.

Ясно, что 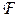- это отображение «многих в одно». Множество эквивалентности, определяемое преобразованием 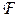, содержит функции времени, отличающиеся лишь на конечном множестве точек в любом интервале времени. Такие разрывные сигналы не имеют практического значения, поэтому обычно рассматривают множество эквивалентности как один сигнал. Эта эквивалентность означает равенство почти всюду, и мы не будем различать сигналы и соответствующие им множества эквивалентности, определяемые равенством «почти всюду». Т. е. будем считать, что 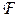взаимно-однозначное отображение.

Обратное отображение задается соотношением:

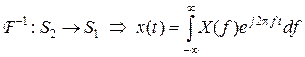. (1.1.10)

Соотношения (1.1.9) и (1.1.10), взятые вместе, называются парой преобразований Фурье.

1.4. Приближенное представление сигналов рядами

Для решения практических задач сигналы часто представляют приближенно в виде рядов, т.е. как непрерывную счетную последовательность функционалов :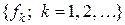

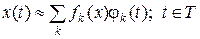, (1.1.12)

где 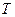- некоторый интервал действительной оси, на котором аппроксимация правомерна, 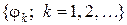- заданное множество сигналов, выбранных независимо от аппроксимируемого сигнала 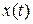. Знак 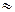указывает на то, что ряд дает приближенное представление.

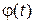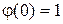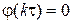Для примера рассмотрим временной ряд, представляющий собой импульс, имеющий различные смещения по оси времени. Импульс будем называть интерполирующим, если он удовлетворяет условиям и для 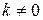, как показано на рис. 1.5.

В этом случае 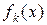будут являться значениями сигнала в моменты времени 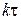, т. е.

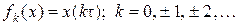(1.13)

Приближенное представление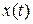

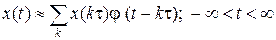. (1.1.14)

В моменты времени 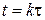будет точное равенство, а в остальные моменты приближение будет тем лучшее, чем медленнее меняется .

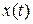Для сигналов с ограниченной полосой 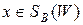согласно теории Котельникова получим, что

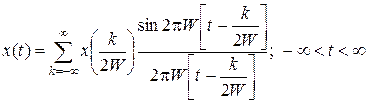, (1.1.15)

где 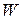- верхняя граничная частота.

Если выборки делаются с частотой 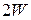(периодом 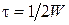), то сигнал будет иметь точное представление рядом, а частота 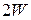называется частотой Найквиста.

Другим распространенным способом представления сигналов рядом является разложение в ряд Фурье. Если 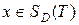(сигнал с ограниченной длительностью) и 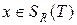(периодический сигнал), то

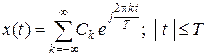, (1.1.16)

где 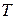- интервал действия сигнала для 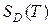и период для 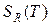. Коэффициенты разложения определяются функционалами

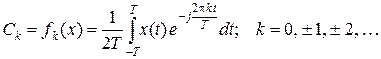(1.1.17)