Лекция 4. Решения полей методом наложения и зеркального отображения. Частичные ёмкости

Пусть мы имеем несколько заряженных проводников с зарядами известной величины Q_i, место расположения которых нам также известно. В этом случае потенциал поля в некоторой произвольной точке будет представлять собой сумму потенциалов, создаваемых каждым из проводников в этой точке:

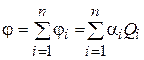(2.27)

Выражение (2.27) справедливо в любой точке поля, в том числе и в месте расположения проводников с зарядами. Потенциал первого проводника определяется суммой:

j₁ = a₁₁Q₁ + a₁₂Q₂ + a₁₃Q₃ + a₁₄Q₄ + … + a_1nQ_n . (2.28)

Первое слагаемое в (2.28) представляет собой потенциал первого проводника, обусловленный зарядом на самом проводнике. Второе слагаемое – потенциал на первом проводнике, обусловленный зарядом Q₂ на втором проводнике и т.д. Коэффициенты a_mn называются потенциальными коэффициентами. Их величина зависит только от формы и взаимного расположения проводников. Так коэффициент a₁₁ численно равен потенциалу на первом проводнике при величине заряда на нем равном 1 (Q₁ = 1), причем заряды других проводников должны равняться нулю. Коэффициент a₁₂ численно равен потенциалу на первом проводнике при величине заряда на втором проводнике равном 1 (Q₂ = 1), причем заряды других проводников должны равняться нулю и т.д. Выражения подобные (2.28) можно записать для любого проводника:

j₁ = a₁₁Q₁ + a₁₂Q₂ + a₁₃Q₃ + a₁₄Q₄ + … + a_1nQ_n

j₂ = a₂₁Q₁ + a₂₂Q₂ + a₂₃Q₃ + a₂₄Q₄ + … + a_2nQ_n

j₃ = a₃₁Q₁ + a₃₂Q₂ + a₃₃Q₃ + a₃₄Q₄ + … + a_3nQ_n (2.29)

……………………………………………………

j_n = a_n1Q₁ + a_n2Q₂ + a_n3Q₃ + a_n4Q₄ + … + a_nnQ_n

_{в векторной форме (2.29) имеет вид} j = a×Q.

Задача расчета потенциалов проводников сводится к определению потенциальных коэффициентов a_mn системы уравнений (2.29).

Чаще приходится решать задачу обратную рассмотренной – находить заряды проводников по известным величинам разностей потенциалов между проводниками. Линейную систему уравнений (2.29) можно переписать в следующей форме:

Q₁ = C₁₁×j₁ + C₁₂×(j₁-j₂) + C₁₃×(j₁-j₃) + … + C_1n×(j₁-j_n)

Q₂ = C₂₁×(j₂ -j₁)+ C₂₂×j₂ + C₂₃×(j₂-j₃) + … + C_2n×(j₂-j_n)

Q₃ = C₃₁×(j₃ -j₁)+ C₃₂××(j₃-j₂) + C₃₃×j₃ + … + C_3n×(j₃-j_n) (2.30)

…………………………………………………………….

Q_n = C_n1×(j_n-j₁) + C_n2×(j_n-j₂) + C_n3×(j_n-j₃) + … + C_nn×j_n

_{в векторной форме (2.30) имеет вид} Q = a^-1×j,

где C = a^-1- обратная (инверсная) матрица к матрице потенциальных коэффициентов.

Коэффициенты С_mn в системе уравнений (2.30) называются частичными емкостями. Так коэффициент С₁₁ численно равен заряду на первом проводнике, когда потенциалы всех проводников равны между собой и равны единице. Коэффициент С₁₂ численно равен заряду на первом проводнике, когда все проводники кроме второго заземлены (их потенциал равен нулю), а потенциал второго проводника равен –1.

Потенциальные коэффициенты в (2.29) и частичные емкости в (2.30) образуют симметричные относительно главной диагонали квадратные действительные матрицы: a_mn = a_nm, C_mn = C_nm. Это свойство вытекает из самих определений потенциальных коэффициентов и частичных емкостей. Пусть на проводник под номером n поместили заряд Q_n=1, а на всех остальных проводниках заряды равны нулю. Потенциал проводника под номером m будет равен j_m = a_mnQ_n = a_mn×1. Величина этого наведенного в проводнике m потенциала будет определяться только взаимным расположением и формой проводников m и n. Если теперь, не изменяя взаимного расположения проводников, заряд Q=1 перенести на проводник m, то потенциал, наведенный на проводнике n, будет иметь ту же величину, что ранее был на проводнике m. В результате a_mn = a_nm.

Величина частичной емкости между проводниками m и n зависит только от их формы и взаимного расположения. Частичные емкости удобно определять опытным путем.

Ёмкость проводника определяется отношением заряда на проводнике к его потенциалу. Для определения ёмкости проводника относительно земли нужно заряд на нем разделить на напряжение относительно земли.