Представление сигналов как элементов множеств

Как уже отмечалось, при графическом представлении сигнал изображается обычно графиком. Рассмотрим другое представление, при котором каждый сигнал изображается в пространстве сигналов точкой. В этом случае сигнал можно считать элементом некоторого множества 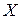со свойством 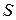, которое справедливо для всех сигналов из множества 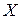. 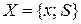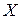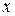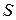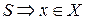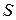Условно это можно изобразить как : - множество всех сигналов , для которых выполнено свойство , или : верно для всех сигналов 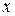, принадлежащих множеству ».

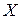Таким образом, свойство 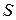задает множество сигналов. Отметим, что выбор свойства 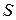является непростой задачей, поскольку с одной стороны проще работать с множеством малой мощности (содержащим небольшое число сигналов), с другой же стороны в нем может не отыскаться нужных нам сигналов.

Рассмотрим несколько примеров множеств сигналов, которые наиболее часто используются на практике:

Периодические сигналы. Множество периодических сигналов с периодом 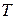обозначим через

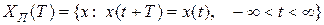. (1.1.1)

Гармонические сигналы. Множество всех гармонических (т.е. синусоидальных) сигналов обозначим через 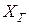, тогда

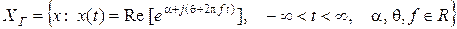, (1.1.2)

где 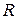- множество действительных чисел, а 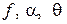- определяют частоту, амплитуду и начальную фазу всевозможных гармонических колебаний.

Сигналы с ограниченным уровнем. Множество сигналов, мгновенные значения которых ограничены по величине некоторым положительным вещественным числом 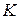, обозначим

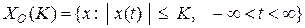. (1.1.3)

При этом очевидно, что если 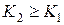, то

.

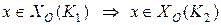Сигналы ограниченной длительности. Сигналы, которые равны нулю за пределами интервала времени 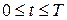, обозначим

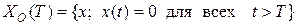. (1.1.4)

При этом очевидно, что если 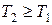, то

.

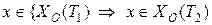Сигналы с ограниченной полосой частот. Если максимальная частота сигнала не превышает по модулю значения 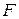, то множество сигналов с ограниченной полосой частот можно записать как

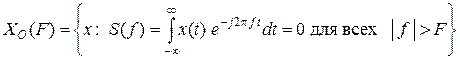, (1.1.5)

где 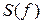- преобразование Фурье от сигнала .

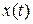Сигналы с ограниченной энергией. Это такие сигналы, энергия которых не превышает некоторой величины 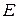, где 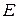- вещественное положительное число. Обозначим множество таких сигналов через

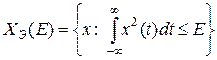, (1.1.6)

Интеграл в (1.1.5) в физическом смысле трактуют как энергию. Например, если 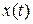- напряжение на нагрузочном сопротивлении 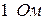, то интеграл по времени от квадрата этого напряжения соответствует полной энергии, выделяющейся на этом сопротивлении.

Отметим, что свойство 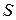для конкретного множества можно указать и в неявной форме, например для гармонических сигналов

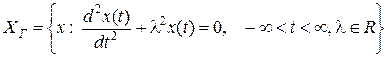. (1.1.7)