Представление сигналов как функций времени и частоты
Очень часто сигналами являются величины, изменяющиеся во времени. Поэтому наиболее распространенной формой представления сигнала является функция времени 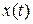 . В свою очередь, привычным способом представления временной функции является ее графическое изображение. График - этосовокупность упорядоченных пар значений,
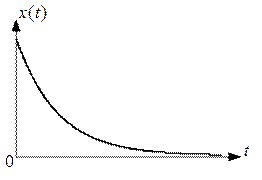
. В свою очередь, привычным способом представления временной функции является ее графическое изображение. График - этосовокупность упорядоченных пар значений, 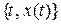 в декартовой системе координат, взятых достаточно плотно. (Можно пример -экспанента) В дальнейшем если это не приводит к двусмысленности, то в зависимости от контекста под символом
в декартовой системе координат, взятых достаточно плотно. (Можно пример -экспанента) В дальнейшем если это не приводит к двусмысленности, то в зависимости от контекста под символом 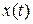 будем понимать как саму функцию
будем понимать как саму функцию 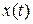 , т.е. правило по которому каждому значению
, т.е. правило по которому каждому значению 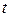 ставится в соответствие величина
ставится в соответствие величина 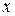 , так и величину, равную значению функции в момент времени
, так и величину, равную значению функции в момент времени 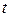 .
.
Функционалы
Преобразование достаточно общих сигналов в числовые значения особенно важно потому, что физические измерения сигналов дают некоторые их числовые характеристики. Отображение произвольного множества в множество чисел часто называют функцией. Но в наших приложениях исходными элементами часто являются функции в обычном смысле (т.е. отображения одного множества чисел в другое множество, например, функции времени, функции частоты и др.). Отображение множества обычных функций в числовые значения принято называть функционалами. Таким образом, под функционалом понимают «функцию от функции».
Заметим, что под числами понимается не только множество 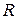 действительных чисел, но и множество
действительных чисел, но и множество  комплексных чисел, хотя это не имеет прямой связи с физическими измерениями. Заметим также, что каждому комплексному числу могут быть сопоставлены два вещественных числа.
комплексных чисел, хотя это не имеет прямой связи с физическими измерениями. Заметим также, что каждому комплексному числу могут быть сопоставлены два вещественных числа.
Приведем для примера несколько типичных функционалов.
Обозначим через 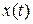 - сигнал,
- сигнал, 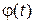 - плотность распределения вероятностей,
- плотность распределения вероятностей, 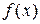 - математическое ожидание
- математическое ожидание
1) 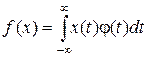 ;
;
2) 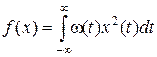 ;
;
3) 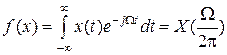 ;
;
4) 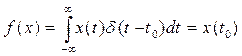 ; (1.1.11)
; (1.1.11)
5) 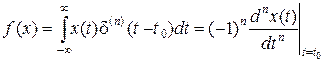 ;
;
6) 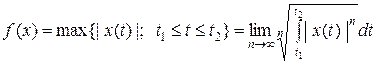 .
.
Как правило, все наиболее употребительные функционалы выражаются через интегралы, такая форма функционала наиболее удобна и применяется даже тогда, когда содержит особые (обобщенные) функции, такие, как 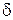 -функция в 4) и 5), требующие специального определения, чтобы функционал имел смысл.
-функция в 4) и 5), требующие специального определения, чтобы функционал имел смысл.
Другим широко распространенным в технических приложениях представлением сигналов является их представление как функций частоты 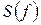 . Графическим представлением частотной зависимости (зависимости спектральной плотности от частоты) также является график. Представление сигнала как функции частоты и как функции времени связаны между собой преобразованием Фурье
. Графическим представлением частотной зависимости (зависимости спектральной плотности от частоты) также является график. Представление сигнала как функции частоты и как функции времени связаны между собой преобразованием Фурье
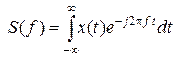 .
.
Преобразование Фурье широко применяется в теории сигналов и справедливо для сигналов с ограниченной энергией, т.е. при
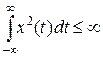 . (1.1.10а)
. (1.1.10а)
Обратное преобразование из частотного представления сигнала во временное представление можно выполнить с помощью обратного преобразования Фурье
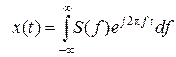 . (1.1.10)
. (1.1.10)
Соотношения (1.1.10а) и (1.1.10) называют также парой преобразований Фурье.
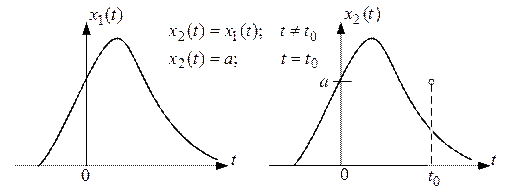
Если подходить строго, то преобразование Фурье не является взаимно-однозначным, т.к. может существовать две и более функций времени, отличающихся на конечном множестве точек в любом интервале времени для которых преобразования Фурье одинаковы. Отличие значений функций на конечном множестве точек иногда называют «равенством почти всюду». Пример таких функций приведен на рис. 1.4. Однако такие разрывные сигналы практического значения не имеют, т.к. для их получения потребовалась бы бесконечно большая мощность, которой реальные источники не обладают. Поэтому преобразование Фурье (а точнее соответствие между функциями с интегрируемым квадратом и их преобразованиями Фурье) считают обычно взаимно-однозначным преобразованием.
С учетом симметричной природы прямого и обратного преобразования Фурье каждому отношению временных функций соответствует дуальное отношение их Фурье-преобразований. Это свойство получило название частотно-временной дуальности. Решая любую задачу по обработке сигналов во временной области мы автоматически получаем решение дуальной задачи в частотной области. Примеры использования частотно-временной дуальности будут приведены в разделе ***
Дата добавления: 2016-11-04; просмотров: 2923;











