Свойства функции полезности.
Функция полезности удовлетворяет свойствам:
- возрастание потребления одного продукта при постоянном потреблении другого продукта введет к росту потребительской оценки, т.е.
если 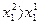 , то U
, то U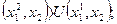
если 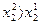 , то U
, то U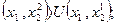
1`. 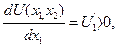
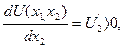
Из свойства 1` следует свойство 1.
Опр. Первые частные производные называют предельными полезностями продуктов:
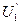 - предельная полезность первого продукта,
- предельная полезность первого продукта,
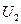 - предельная полезность второго продукта.
- предельная полезность второго продукта.
Используется символика:
M1U(x1,x2), M2U(x1,x2)
- Предельная полезность каждого продукта уменьшается, если объём его потребления растёт (это свойство называют законом убывающей предельной полезности).
2`. 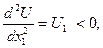

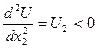 ;
;
Из свойства 2` следует свойство 2.
- Предельная полезность каждого продукта увеличивается, если растет количество другого продукта. В этом случае продукт количество которого фиксировано, оказывается относительно дефицитным. Поэтому дополнительная его единица приобретает большую ценность и может быть потреблена более эффективно. Данное свойство не столь очевидно как 1 или 2, и справедливо не для всех благ: если блага могут полностью замещать, друг друга в потреблении свойства 3 не выполняется.
Предположение 3 вводится не всегда, но оно гарантирует выпуклость вниз линии безразличия.
3`. 
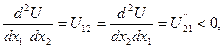
Из свойства 3` следует свойство 3.
Опр. Под предельной полезностью первого(второго) продукта понимают отношении приращения функции полезности к приращению вызвавшего его количество этого продукта:
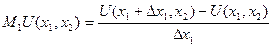 или
или
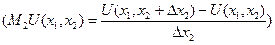 .
.
Тогда предельную полезность первого (второго) продукта называют разность:
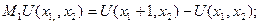
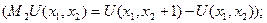 или
или
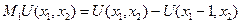 ;
; 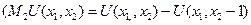 .
.
Рассмотрим фиксированную линию безразличия l. Пусть потребительский набор (x1,x2) 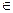 l. При выполнении предположений: непрерывность первых частных производных
l. При выполнении предположений: непрерывность первых частных производных 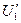 ,
, 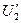 и
и 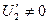 справедлива формула:
справедлива формула:
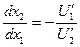 (1)
(1)
Рассмотрим рисунок Рис.2.
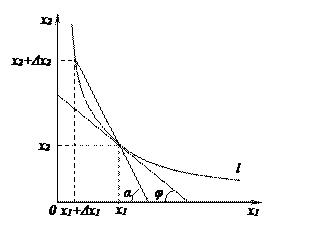
Рис.2.
Имеем приближенное равенство
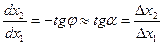 (2)
(2)
Из (1) и (2) вытекает приближенное равенство:
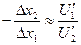
Отношение 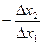 показывает, на сколько должен индивидуум увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей.
показывает, на сколько должен индивидуум увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей.
Это обстоятельство геометрически представлено так: точки (х1, х2), (х1+Δх1, х2 +Δх2) принадлежат одной и той же линии без различия l.
Опр. Дробь: 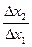 принято называть нормой замены первого продукта вторым на потребительском наборе (х1, х2),а производную
принято называть нормой замены первого продукта вторым на потребительском наборе (х1, х2),а производную 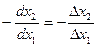 при
при 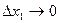 предельной нормой замены первого продукта вторым.
предельной нормой замены первого продукта вторым.
Пример
Пусть функция полезности выражается через функцию:
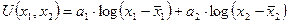 ,
,
где 
Тогда имеем
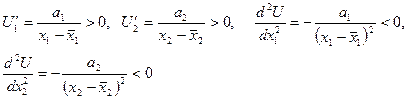
т.е. свойства 1' и 2' функции полезности выполнены.
Свойство 3΄, не выполнено, так смешанные вторые частные производные функции U (х1, х2) равны нулю.
Задача потребительского выбора (задача рационального поведения потребителя на рынке) заключается в выборе такого потребительского набора (х10, х20), который максимизирует его функцию полезности при заданном бюджетном ограничении.
Бюджетное ограничение означает, что денежные расходы на продукты не могут превышать денежного дохода, т.е. р1х1 + р2х2 ≤ I, где р1, р2 – рыночные цены одной единицы первого и второго продуктов соответственно, а I – доход индивидуума, который он готов потратить на приобретение первого и второго продуктов, Величины р1, р2, I – заданы (экзогенные).
Формально задача потребительского выбора имеет вид:
U (х1, х2) → (max)
р1х1 + р2х2 ≤ I (3)
х1 ≥ 0, х2 ≥ 0
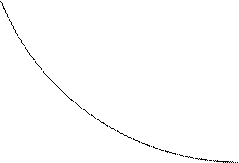
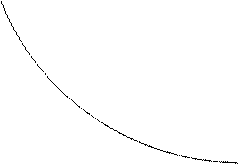 Допустимое множество (то есть множество наборов благ, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой (рис.2).
Допустимое множество (то есть множество наборов благ, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой (рис.2).
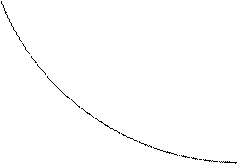


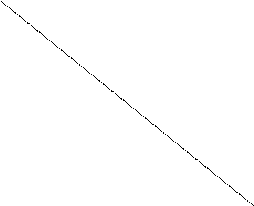

 х2 бюджетная прямая
х2 бюджетная прямая
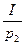

 Линия безразличия
Линия безразличия
(х10, х20)
O 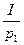
Рис.2
На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности. Поиск этой точки можно интерпретировать графически как последовательный переход на линии все более высокого уровня полезности (вправо – вверх) до тех пор, пока эти линии еще имеют общие точки с допустимым множеством.
Набор (х10, х20), которой является решением задачи потребительского выбора, принято называть оптимальным равновесием потребителя или локальным рыночным равновесием потребителя.
Дата добавления: 2021-02-19; просмотров: 521;











