Пример задачи потребительского выбора

Пусть неизвестные количества благ равны х₁ и х₂, а их рыночные цены р₁ и р₂:

U (х₁, х₂) = х₁ х₂ → max

р₁х₁ + р₂х₂ ≤ I

х₁ ≥ 0, х₂ ≥ 0,

Бюджетное ограничение в оптимальной точке должно выполняться как равенство, и поскольку ода блага жизненно необходимы (полезность равна нулю, если одно из них отсутствует), требования неотрицательности переменных будут выполнены автоматически. Следовательно, решаемая задача математического программирования превращается в классическую задачу на условный экстремум. Запишем необходимые условия экстремума: отношения предельных полезностей благ должны равняться отношениям их рыночных цен, а бюджетное ограничение выполняется как равенство.

Получим систему уравнений:

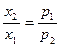
р₁х₁ + р₂х₂ = I

Первое условие означает, в задаче количество денег на оба блага, должны быть одинаковыми,

то есть х₂ р₂ = х₁ р₁.

Это вытекает из равенства «весов», или показателей степени у переменных х₁ и х₂ в функциях полезности.

Итак

х₂ р₂ = р₁ х₁ =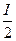

и функция спроса приобретает вид:

х₁ = 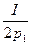; х₂ = .

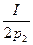Расход на каждое благо составляет половину дохода потребителя, и чтобы найти необходимое количество каждого блага, следует разделить расходуемую на него сумму на его цену.

Самостоятельно для этой простой модели найти решение без использования метода множителей Лагранжа, выражая х₂ через х₁ из бюджетного ограничения, подставляя это выражение в функцию полезности (которая становится полиномом второй степени от одной переменной) и находя максимум полученной квадратичной функции.