Решение задачи потребительского выбора

Задачу потребительского выбора заменим задачей на условный экстремум:

U (х₁, х₂) → max

при условии (4)

р₁х₁ + р₂х = I

Для решения задачи применим метод Лагранжа.

Выписываем функцию Лагранжа:

L (х₁, х₂, λ) = U (х₁, х₂) + λ (р₁х₁ + р₂х₂ – I), (5)

находим ее первые частные производные по переменным х₁, х₂, λ; приравниваем эти частные производные к нулю:

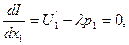
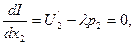
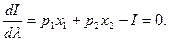
Исключив из полученной системы трех уравнений с тремя неизвестными, неизвестную λ, получим систему двух уравнений с двумя неизвестными х₁ и х₂

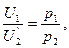
р₁х₁ + р₂х₂ = I.

Решение (х₁⁰, х₂⁰) этой системы есть «укороченная» критическая точка функции Лагранжа.

Можно строго доказать, что «укороченная» критическая точка (х₁⁹, х₂⁰) функции Лагранжа обязательно есть решение задачи потребительского выбора (за исключением так называемых угловых решений, которые не рассматриваются).

Подставив решение (х₁⁹, х₂⁰) в левую часть равенства

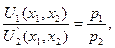(6)

получим что в точке (х₁⁰, х₂⁰) локального рыночного равновесия индивидуума отношение предельных полезностей U₁́(х₁⁰, х₂⁰) и U₂́(х₁⁰, х₂⁰) продуктов равно отношению рыночных цен р₁ и р₂ на эти продукты:

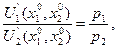
В связи с тем, что отношение 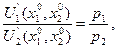равно предельной норме за-

мены первого продукта вторым в точке локального рыночного равновесия (х₁⁰, х₂⁰) из (6) следует, что эта предельная норма равна отношению рыночных цен 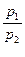на продукты. Приведенный результат играет важную роль в экономической теории.

Геометрически решение (х₁⁰, х₂⁰) можно интерпретировать как точку касания линии безразличия функции полезности U(х₁, х₂) с бюджетной прямой р₁х₁ + р₂х₂ = I (рис.2). Это определяется тем, что отношение

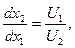показывает тангенс угла наклона бюджетной прямой.

Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание двух линий.