Классификация моделей в экономике

Математические модели, используемые в экономике можно подразделить на классы по ряду признаков, относящихся к:

1. особенностям моделируемого объекта;
2. цели моделирования;
3. используемого инструментария.

Выделяют следующие классы моделей:

1. Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: ВВП, потребление, инвестиции, занятость, процентную ставку, количество денег и т.д.

2. Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде. В следствии разнообразия типов экономических элементов и форм их взаимодействия на рынке, микроэкономическое моделирование занимает основную часть экономико-математической тории. Наиболее серьезные теоретические результаты здесь получены в последние годы в исследовании стратегического поведения с использованием аппарата теории игр.

3. Теоретические модели позволяют изучать общие свойства экономики и ее характерных элементов дедукцией видов из формальных предпосылок.

4. Прикладные модели дают возможность оценить параметры функционирования конкретного экономического объекта и сформулировать рекомендации для принятия практических решений. К прикладным относятся прежде всего экономические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений.

5. Равновесные модели – описывают такие состояния экономики, когда результирующее всех сил стремящихся вывести ее из данного состояния равна нулю. В непрерывной экономике неравновесие по одним параметрам (например дефицит) компенсируется другими факторами (черный рынок, очереди и т.д.). Равновесие модели дескриптивны, описательны. Оптимизация в теории рыночной экономики присутствуют в основном на микроуровне (максимализация полезности потребления или прибыли фирмы); на макроуровне результатом рационального выбора поведения экономическими субъектами оказывается некоторое состояние равновесия.

6. Статические модели описывают состояние экономического объекта в конкретный момент или период времени. В статических моделях обычно зафиксированы значения ряда величин являющихся переменными в динамике, например цен, капитальных ресурсов и т.п.

7. Динамические модели включают взаимосвязи переменных во времени. Динамическая модель не сводится к простой сумме ряда статических, и описывает силы и взаимодействия в экономике, определяющей ход процесса в ней. Динамические модели обычно используют аппарат дифференциальных и разностных уравнений, вариационного исчисления.

8. Детерминированные модели предполагают жесткие функциональные связи между переменными модели.

9. Стохастические модели допускают наличие случайных воздействия на исследуемые показатели и используют инструментарий теории вероятности и математической статистике для их описания.

1. Теория потребительского поведения

Пусть потребитель располагает доходом I , который он полностью тратит на приобретение благ (продуктов).

Уточним I – это не доход, а расход данного потребителя. Потребитель решает статистическую задачу, т.е. в модели не учитываются его межвременные предпочтения и возможности делать и расходовать сбережения. Цели благ считаются заданными. Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенные количества благ.

Опр. Математическая модель такого поведения называется моделью потребительского выбора.

Пусть даны наборы двух потребительских благ. Потребительский набор – вектор (х₁, х₂), где х₁ – количество единиц первого блага, х₂ – количество единиц второго блага.

Выбор потребителя (индивидуума) характеризуется отношением предпочтения: считается, что потребитель про каждые два набора может сказать, что-либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы.

На множество потребительских наборов (х₁, х₂) определена функция U( х₁, х₂) ­– называемая функция полезности потребителя, значение U(х₁, х₂) – равно потребительской оценке индивидуума для этого набора. Потребительскую оценку U(х₁, х₂) набора (х₁, х₂) – называют уровнем или степенью удовлетворения потребностей индивидуума, если потребитель приобретает или потребляет данный набор (х₁, х₂).

Каждый потребитель имеет свою функцию полезности. Если набор А предпочтительнее набора В, то U(A)> U(B).

Опр. Линия, соединяющая потребительские наборы (х₁, х₂), имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линией безразличия.

Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия, соответствующие разным уровням удовлетворения потребностей называется картой линий безразличия.

x2

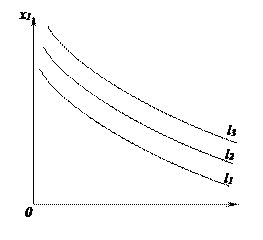
Рис.1