Спектры последовательности прямоугольных импульсов.

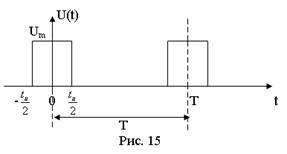
Рассмотрим периодическую последовательность импульсов прямоугольной формы с периодом Т, длительностью импульсов t_u и максимальным значением 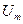. Найдем разложение в ряд такого сигнала, выбрав начало координат, как показано на рис. 15. При этом функция симметрична относительно оси ординат, т.е. все коэффициенты синусоидальных составляющих 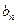=0, и нужно рассчитать только коэффициенты .

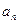(2.27)

постоянная составляющая

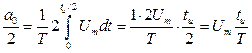(2.28)

Постоянная составляющая – это среднее значение за период, т.е. это площадь импульса 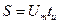, деленная на весь период, т.е. 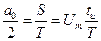, т.е. то же, что получилось и при строгом формальном вычислении (2.28).

Вспомним, что частота первой гармоники ¦₁= 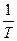, где Т – период прямоугольного сигнала. Расстояние между гармониками D¦=¦₁. Если номер гармоники n окажется таким, что аргумент синуса 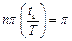, то амплитуда этой гармоники первый раз обращается в нуль. Это условие выполняется при 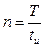. Номер гармоники, при котором амплитуда ее обращается в ноль первый раз, называют «первым нулем» и обозначают его буквой N, подчеркивая особые свойства этой гармоники:

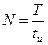(2.29)

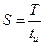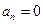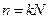С другой стороны, скважность S импульсов – это отношение периода Т к длительности импульсов t_u, т.е. . Следовательно «первый нуль» численно равен скважности импульса N=S. Поскольку синус обращается в ноль при всех значениях аргумента, кратных p, то и амплитуды всех гармоник с номерами, кратными номеру «первого нуля», тоже обращаются в ноль. То есть при , где k – любое целое число. Так, например, из (2.22) и (2.23) следует, что спектр прямоугольных импульсов со скважностью 2 состоит только из нечетных гармоник. Поскольку S=2, то и N=2, т.е. амплитуда второй гармоники первый раз обращается в ноль – это «первый нуль». Но тогда и амплитуды всех остальных гармоник с номерами, кратными 2, т.е. все четные тоже должны обращаться в ноль. При скважности S=3 нулевые амплитуды будут у 3, 6, 9, 12, ….гармоник.

С увеличением скважности «первый нуль» смещается в область гармоник с большими номерами и, следовательно, скорость убывания амплитуд гармоник уменьшается. Простой расчет амплитуды первой гармоники при U_m=100В для скважности S=2, U_m1=63,7B, при S=5, U_m1=37,4B и при S=10, U_m1=19,7B, т.е. с ростом скважности амплитуда первой гармоники резко уменьшается. Если же найти отношение амплитуды, например, 5-й гармоники U_m5 к амплитуде первой гармоники U_m1, то для S=2, U_m5/U_m1=0,2, а для S=10, U_m5/U_m1=0,9, т.е. скорость затухания высших гармоник с ростом скважности уменьшается.

Таким образом, с ростом скважности спектр последовательности прямоугольных импульсов становится более равномерным.