Спектральное представление сигналов.

Совокупность гармонических составляющих, образующих негармонический сигнал, называется спектром этого сигнала. Спектр можно было бы представить графически в виде совокупности временных кривых входящих в него гармоник, но такое изображение громоздко и малонаглядно, поэтому не используется. Вместо этого принято изображать спектр сигнала в виде линейчатой диаграммы, в которой на оси частот наносятся вертикальные отрезки, длина которых пропорциональна амплитуде данной гармоники, а её положение на оси частот определяется номером гармоники. Например, если некоторый периодический сигнал описывается рядом

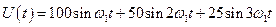, то спектр этого сигнала представляет рис.12.

На этом спектре показаны соотношения амплитуд спектральных составляющих сигнала, поэтому спектр называется амплитудным. Аналогично можно строить фазные спектры, на которых по оси частот откладывают начальные фазы гармоник также в виде вертикальных отрезков в выбранном масштабе.

Так как ряд любого периодического сигнала состоит из гармоник, частоты которых в целое число раз отличаются от частоты первой гармоники, то спектральные линии находятся на одинаковом расстоянии Dw друг от друга (или D¦), которое равно частоте основной гармоники w₁ (или ¦₁). Спектры, состоящие из отдельных линий, называются дискретными или линейчатыми.

Приведем примеры спектров некоторых рассмотренных нами сигналов. Из (2. 21) следует, что сигналы треугольной формы состоят из гармоник с нечетными номерами, амплитуды которых убывают пропорционально квадрату номера гармоники. Амплитуды в спектрах можно строить в относительных единицах. Если принять амплитуду первой гармоники за 1, то амплитуда второй гармоники , амплитуда 3-й гармоники в 1/3² меньше, чем первой, т.е. , , и т.д. Спектр этого сигнала на рис. 13.

Из (2.22) спектр сигналов прямоугольной формы со скважностью 2 состоит из нечетных гармоник, амплитуды которых убывают пропорционально номерам гармоник. Поэтому амплитуды всех четных гармоник также равны нулю, а амплитуды нечетных гармоник по отношению к амплитуде первой гармоники, принятой за 1, будут выражаться: 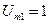; ; 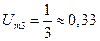…… Спектр на рис. 14