Примеры разложения в ряд Фурье реальных сигналов.

Приведем разложения в ряд Фурье некоторых, наиболее часто встречающихся периодических сигналов.

а). Сигнал на выходе однополупериодного выпрямителя (рис. 5)

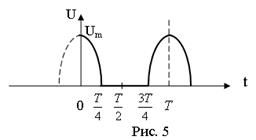
(2.18)

б). Сигнал на выходе двухполупериодного выпрямителя (рис. 6)

(2.19)

в). Сигнал треугольной формы (рис. 7а, б)

(2.20)

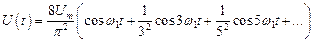(2.21)

г). Сигнал прямоугольной формы со скважностью 2 (меандр) (рис.8 а, б)

(n – целое, нечетное) (а) (2.22)

(б) (2.23)

Сигналы рис. 8 а, б идеализированы, т.к. имеют фронты бесконечно малой длительности. Практически такие сигналы не существуют, в точках разрыва, как отмечалось, ряды (2.22) и (2.23) не сходятся, но в среднем сходимость ряда обеспечивается.

д). Сигналы трапецеидальной формы (рис. 9).

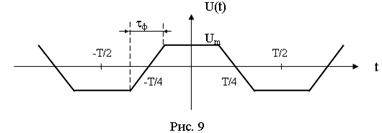
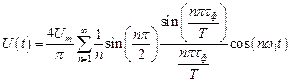(2.24)

обычно t_ф << Т, поэтому при малых n множитель .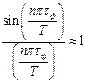

При этом амплитуды нескольких первых гармоник рядов (2.23) и (2.24) почти одинаковы. Но с ростом n амплитуды гармоник ряда (2.24) убывают быстрее, чем у ряда (2.23). Ряд Фурье для реального сигнала рис. 9 сходится быстрее.

е). Пилообразный сигнал (рис. 10).

Такой формы напряжение используется в схемах развертки осциллографа, телевизора, монитора. Ряд Фурье этого сигнала:

(2.25)

ж). Последовательность коротких прямоугольных видеоимпульсов (рис.11)

(2.26)

здесь S = Т/τ_и - скважность импульса.

з). Амплитудно-модулированный (АМ) сигнал при гармоническом законе модуляции.

(2.26^/)

где - частота несущего колебания, 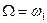- частота гармонического сообщения.