Вычисление плоских прямоугольных координат по геодезическим и наоборот.

На рисунке 33 показан треугольник DCQ на поверхности эллипсоида и его изображение D'C'Q' на плоскости проекции. Геодезические линии DC, CQ и DQ, образующие этот треугольник, изобразятся на плоскости в виде кривых D'C', C'Q' и Q "D", углы между которыми в силу равноугольности проекции Гаусса будут равны соответствующим углам β₁, β₂ и β₃ между геодезическими линиями на поверхности эллипсоида. Меридиан DH изобразится на плоскости проекции также в виде кривой D'H', составляющей с линией, параллельной оси х, угол γ, называемый сближением меридианов на плоскости. При этом азимут А геодезической линии DQ будет равен углу на плоскости проекции между изображениями меридиана D'Н' и геодезической линии D'Q'.

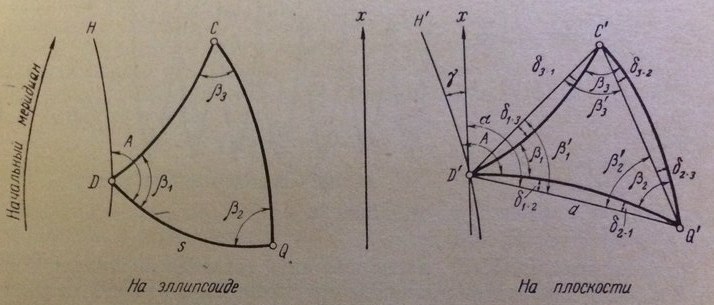
Чтобы получить возможность применить формулы плоской тригонометрии для решения треугольников, образованных изображениями геодезических линий, необходимо предварительно перейти от сфероидических углов к углам между хордами, проведенными через изображения вершин треугольников на плоскости проекции. Для этого достаточно учесть небольшие поправки δ, называемые поправками за кривизну изображения геодезических линий. На рисунке видно, что угол β₁' между хордами D'C' и D'Q' равен

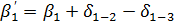
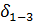имеет знак минус.

Необходимо также вычислить плоские координаты x и y исходного пункта по данным его геодезическим координатам B и L.

Исходный дирекционный угол α получается по формуле:

α = А – γ + δ

Плоское сближение меридианов γ вычисляется по геодезическим координатам В и L или по плоским координатам х и y.

Если известна длина геодезической линии s на поверхности эллипсоида, то возникает задача редуцирования ее на плоскость проекции, заключающаяся в нахождении длины хорды d. Это осуществляется введением в s небольшой поправки .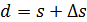

Поправки δ и 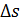вычисляют по приближенным плоским координатам, которые находят используя неисправленные длины и сфероидические углы. Таким образом, вычисления приходится вести последовательными приближениями:

1. сначала найти приближенные координаты,

2. по ним вычислить поправки δ и ,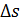

3. редуцировать измеренные углы и длины на плоскость проекции и затем уже найти точные значения координат пунктов.

Очевидно, необходим и обратный переход с плоскости проекции на поверхность эллипсоида. В этом случае приходится находить геодезические координаты B и L, азимуты А, сфероидические углы β и длины геодезических линий s по данным плоским координатам х и y, дирекционным углам α, плоским углам β' и длинам хорд d.

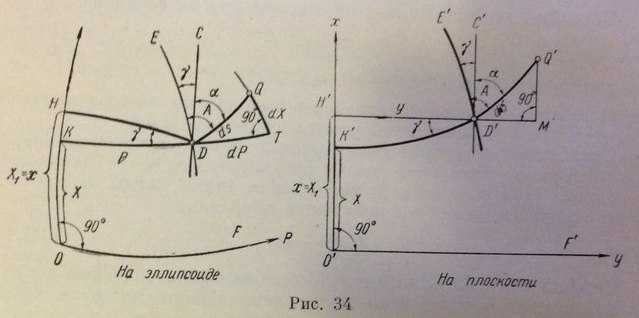
На рис. 34 показаны две бесконечно близкие точки D и Q на поверхности эллипсоида и их изображения D'Q' на плоскости проекции. Начальный меридиан ОН и экватор OF изображаются на плоскости прямыми линиями О'Н' и O'F', являющимися осями координат; ED и КТ меридиан и параллель точки D, a E'D' и К'D' их изображениями на плоскости; DН – изображение на поверхности эллипсоида линии D'Н', перпендикулярной к оси x. Масштаб проекции вдоль осевого меридиана равен единице и поэтому ОН =О'Н' = X₁=x и ОК=О'К'=X. Обозначим геодезические координаты точки D через В и L, долготу осевого меридиана через L₀, и разность долгот L - L₀ через l. Масштаб проекции в точке D будет

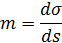
В системе координат Гаусса – Крюгера масштаб вдоль осевого меридиана равен единице и при l = 0 ордината у = 0. Поэтому при l = 0 абсцисса х равна длине дуги меридиана от экватора до параллели с широтой В

x = X = f(q).