Эмпирические формулы

Пусть даны табличные значения 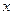и .

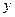Необходимо найти аналитическую зависимость 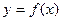. Поиск такой зависимости называют «сглаживанием» экспериментальных данных. Сглаживание можно производить, используя метод наименьших квадратов (МНК). При этом следует указать вид эмпирической формулы

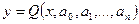(1)

Затем находится сумма квадратов отклонений

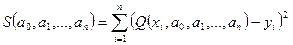(2)

и ищется ее минимум из условий 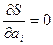, 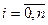(3)

В общем случае система уравнений (3) нелинейна. Ее можно решить, применяя итерационные методы.

1. Более простым методом является метод выравнивания, при котором нелинейнаязависимость (1) может быть сведена к линейной.

Пусть экспериментальные точк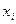и и 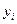не располагаются вблизи прямой. Это свидетельствует о нелинейной зависимости между 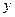и 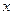. Вводятся новые переменные

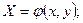
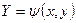. (4)

так, чтобы преобразованные экспериментальные данные 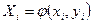; 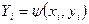менее уклонялись от прямой. Для аппроксимирующей прямой

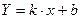(5)

Коэффициент 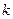и 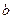можно определить из уравнений (2) и (4)

Окончательный результат получают в виде

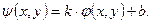(6)

Далее уравнение (6) разрешается относительно .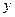

Пример: Установить вид эмпирической формулы 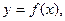используя зависимость (1) с двумя параметрами 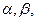и определить наилучшие значения параметров, если данные представлены таблицей

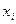
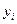
	7.1	27.8	62.1

Решение: Строим график 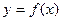. Точки не лежат на прямой.

Делаем преобразование: ; .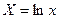

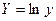Составим таблицу преобразованных данных

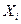
	0.000	0.693	1.099	1.386	1.609
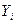
	1.960	3.325	4.128	4.700	5.081

Строим график и убеждаемся, что связь между 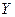и 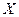почти линейная.

Составляем уравнение

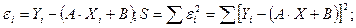
Находим 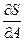и 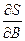, и приравниваем их нулю.

Получаем систему двух уравнений с двумя неизвестными:

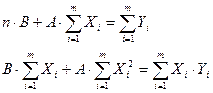
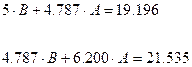
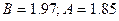
Таким образом

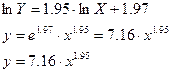
Этот результат можно было бы непосредственно получить, решая задачу

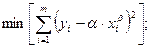
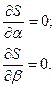
Однако, методом выравнивания задача решается проще!

1. Метод выбранных точек

Обычно применяется для нахождения начальной оценки параметров. Если связь между переменными – нелинейная, то, разлагая нелинейную зависимость в ряд по формуле Тейлора, производят линеаризацию системы, оставляя только линейные члены уравнения. Затем решение уточняется методом итераций. В качестве нулевого (начального) приближения берутся оценки параметров, найденные по методу выбранных точек.

В методе оставляют столько экспериментальных данных, сколько имеется неизвестных параметров.

Затем находится решение полученной системы!