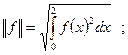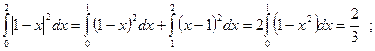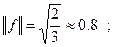Среднеквадратичное приближение функций полиномами Лежандра.
Многочлены Лежандра определяются следующими формулами

Дифференцирую, находим:
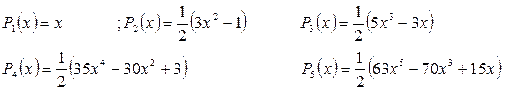
Обобщенный многочлен степени 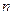 относительно системы алгебраических многочленов Лежандра
относительно системы алгебраических многочленов Лежандра 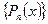 имеет вид
имеет вид
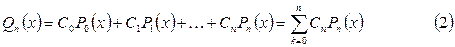
где 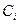 – некоторые постоянные.
– некоторые постоянные.
Система многочленов Лежандра 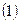 ортогональна на отрезке
ортогональна на отрезке 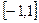
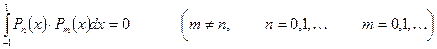
Среднеквадратичная форма 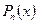 :
:
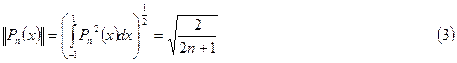
Например: 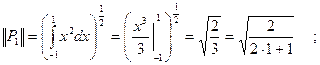
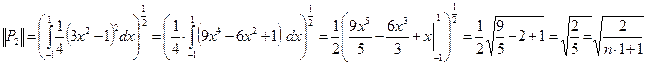
Наилучшее приближение функции 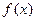 многочленом
многочленом  получается с коэффициентами Фурье:
получается с коэффициентами Фурье:
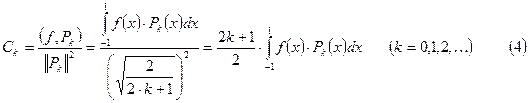
Среднеквадратичное отклонение аппроксимирующего многочлена от функции 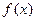 , равное
, равное 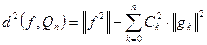 , в нашем случае определяется равенством
, в нашем случае определяется равенством 
Из формулы 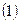 видно, что
видно, что 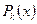 четны при четном
четны при четном 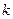 и нечетны при
и нечетны при 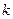 нечетном.
нечетном.
Для четной на интервале 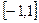 функции
функции 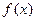 коэффициенты Фурье равны:
коэффициенты Фурье равны:
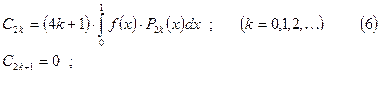
Для нечетной на интервале 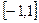 функции получаем:
функции получаем:
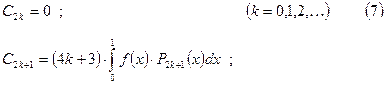
Рядом Фурье – Лежандра называется ряд 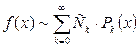
Ряд Фурье – Лежандра сходится к 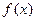 в среднеквадратичном на отрезке
в среднеквадратичном на отрезке 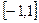 .
.
| Теорема |  Ряд Фурье – Лежандра кусочно-гладкой функции Ряд Фурье – Лежандра кусочно-гладкой функции 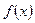 на отрезке на отрезке 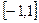 сходится к значению сходится к значению 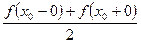 в точке в точке 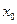 ( сходится к ( сходится к  в точках непрерывности функции). в точках непрерывности функции).
|
Если 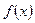 определена на отрезке
определена на отрезке 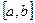 , то с помощью линейного преобразования
, то с помощью линейного преобразования 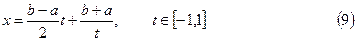
Можно получить многочлены Лежандра, ортогональные на отрезке 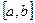 :
:
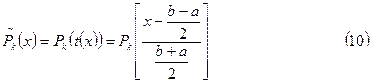
При этом норма 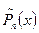 будет равна
будет равна
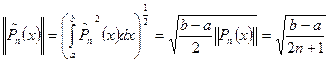
А коэффициенты 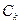 примут вид
примут вид
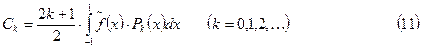
где 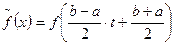
| Пример | Найти алгебраический многочлен степени 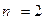 наилучшего среднеквадратического приближения для функции наилучшего среднеквадратического приближения для функции 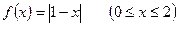 .
Оценить погрешность .
Оценить погрешность 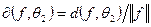 . .
| ||||||
| Решение | Имеем 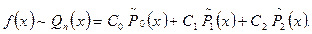 Используя формулы:
Используя формулы: 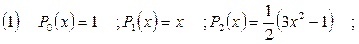
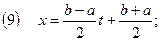
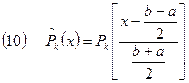 Находим:
Находим: 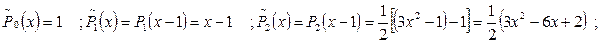 Производя замену переменной по формуле
Производя замену переменной по формуле 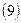 , получим: , получим:
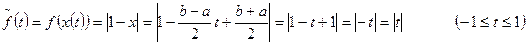 Коэффициенты Фурье вычисляются по формуле
Коэффициенты Фурье вычисляются по формуле 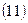
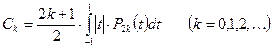 Т.к.
Т.к. 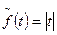 – четная, то можно использовать формулу – четная, то можно использовать формулу 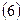
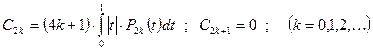 Следовательно
Следовательно
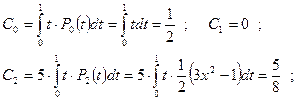 Откуда:
Откуда: 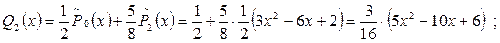 По формуле
По формуле 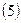 находим погрешность среднеквадратического приближения: находим погрешность среднеквадратического приближения:

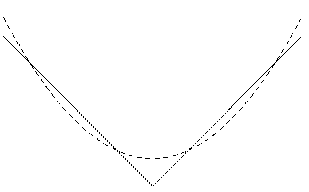
|
Дата добавления: 2016-11-04; просмотров: 4567;


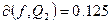 ,
,