Методы численного решения системы линейных алгебраических уравнений.
1. Метод Гаусса(метод исключения неизвестных).
Пример: пусть требуется решить систему уравнений

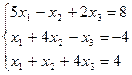 (1)
(1)
Исключим сначала неизвестное х1 из второго и третьего уравнений системы (1), используя первое уравнение. Уравнение, с помощью которого преобразуются остальные уравнения, называют разрешающим, а коэффициент этого уравнения при неизвестном, исключаемом из остальных уравнений, - разрешающим или главным элементом. (Первое уравнение – разрешающее, коэффициент 5 при х1 в этом уравнении – разрешающий элемент).
Разделим первое уравнение на 5 и вычтем преобразованное первое уравнение из второго и третьего уравненийсистемы (1).
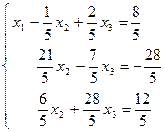

Теперь разрешающее - второе уравнение. Разделим его на 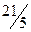 и вычтем преобразованное второе уравнение, умноженное на
и вычтем преобразованное второе уравнение, умноженное на 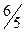 , из третьего уравнения. Получим систему
, из третьего уравнения. Получим систему
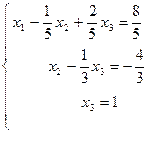
Выполнен прямой ход в методе Гаусса.
Выполняем обратный ход, исключая последовательно 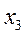 и
и 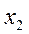 из второго и первого уравнений:
из второго и первого уравнений:
a) умножаем третье уравнение на 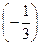 и вычитаем его из второго уравнения;
и вычитаем его из второго уравнения;
b) умножаем его же на 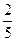 и вычитаем из первого уравнения:
и вычитаем из первого уравнения:
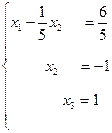
c) умножаем второе уравнение на 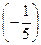 и вычитаем его из первого:
и вычитаем его из первого:
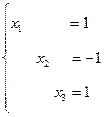 (2)
(2)
Получаем решение системы (1)
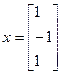
Пусть теперь дана система из n линейных алгебраических уравнений с n неизвестными:
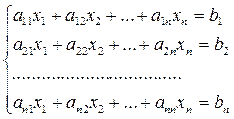 (3)
(3)
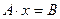
Решением системы (3) называется упорядоченное множество чисел  , если подстановка
, если подстановка 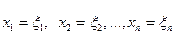 превращает уравнения (3) в равенства
превращает уравнения (3) в равенства 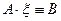 .
.
Дата добавления: 2016-11-04; просмотров: 1496;











