Общая схема метода Гаусса для систем, имеющих единственное решение

Пусть 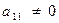. (В противном случае в качестве первого уравнения возьмем какое-либо другое). Разделим первое уравнение на .

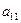Получим

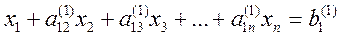, (4)

где ; ,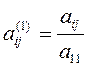

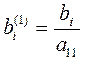
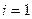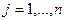
Умножим разрешающее уравнение (4) на 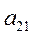и вычтем полученное уравнение из второго уравнения системы (3). Аналогично преобразуем остальные уравнения. Система примет вид

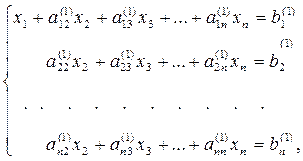(5)

где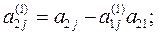

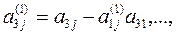
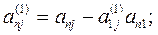
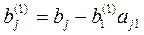
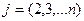
Если какой-либо из коэффициентов 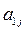окажется равным нулю, то j-ое уравнение системы (3) войдет в систему (5) без изменений т.е.

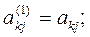
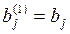
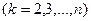
(То есть если в какой-либо из уравнений отсутствовала переменная 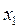, то уравнение не преобразуется). Теперь, оставив без изменения первое уравнение системы (5), сделаем разрешающим второе уравнение и применим описанную процедуру к системе из n-1 уравнений, исключая 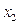из оставшихся уравнений. Получим систему

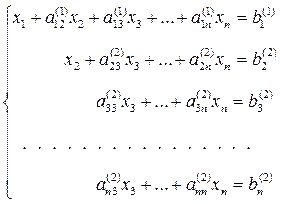
где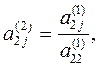

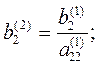
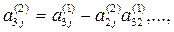
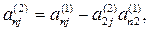
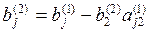
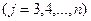
Продолжая аналогичные вычисления, приведем систему (3) к эквивалентной системе с треугольной матрицей коэффициентов

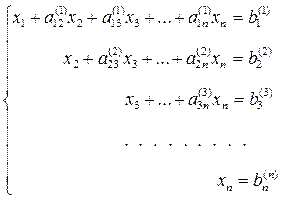(6)

Прямой ход решения выполнен.

Обратный ход:

a) последовательно исключаем неизвестное 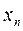, начиная с 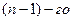уравнения и заканчивая первым. Получаем

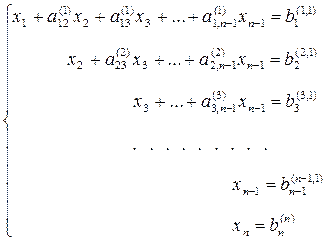(7)

Затем исключаем неизвестное 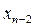из уравнений с номером j

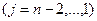и т.д.

В результате получаем решение системы

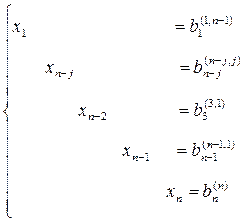
Для уменьшения погрешности вычислений существуют различные модификации метода Гаусса.