Методы расчета константы скорости реакции

Зная порядок реакции, можно рассчитать константу скорости и сделать предположение относительно механизма протекания реакции. Рассмотрим наиболее часто используемые способы определения порядка.

1. Способ подстановки. Экспериментальные результаты поочерёдно подставляют в уравнения константы скорости реакции различных порядков. Если использование одного из этих уравнений даёт постоянную величину константы скорости, реакция имеет соответствующий порядок. Если одинаковые значения не получаются, то реакция имеет дробный порядок или сложный характер.

2. Графический способ. Используя графический метод, уравнение константы скорости реакции приводят к линейному виду и строят график зависимости соответствующей функции концентрации от времени в различных координатах (С_A–τ; lnC_A–τ; 1/C_A–τ; 1/C²_A–τ). Там, где получилась прямая, таков и порядок реакции. По углу наклона прямой к оси ординат определяют значение константы скорости реакции. По длине отрезка, отсекаемого прямой на оси ординат, – начальные концентрации реагирующих веществ.

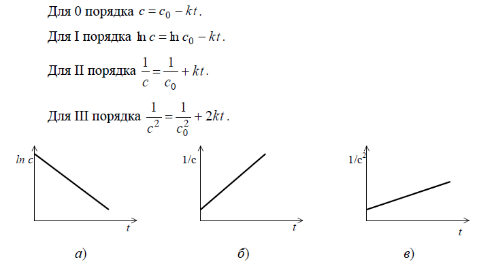
Рис. Зависимость функций концентрации исходных веществ от времени для реакций:

а) первого; б) второго; в) третьего порядков.

3. Способ Оствальда-Нойеса. Основан на определении прядка реакции по периоду полупревращения. Для реакции n-го порядка было получено выражение

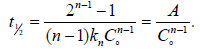
Логарифмируя это выражение, имеем: lg(τ_1/2) = lgA – (n–1)lgC.

Отсюда следует, что зависимость логарифма периода полупревращения от логарифма начальной концентрации вещества представляет собой прямую линию, для которой tg α = (n–1). Отсюда n =1 – tg α.

4.Способ Вант-Гоффа. Необходимо знать две скорости реакции при двух различных концентрациях веществ. v₁ = kC_A1ⁿ и v₂ = kC_A2ⁿ. Тогда

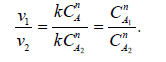
Прологарифмируем: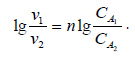
Отсюда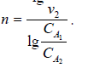

Графический вариант метода Вант-Гоффа: v=k·C_Aⁿ. После логарифмирования получаем: lgv=lgk+n·lgC_A. Порядок реакции n определяют как tg угла наклона прямой в координатах lgv – lgC_A.