Преобразование входных величин с помощью карт Карно

ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ

Законы логического мышления исследовались английским математиком Дж. Булем, который разработал метод проверки истинности определенных высказываний. Понятия истинности и ложности берут свое начало в исчислении высказываний, приводящем к современным методам проектирования с использованием таблиц истинности.

В Булевой алгебре определяется ряд операций, достаточно удобных для использования при логическом конструировании. Логику проектирования удобно представлять математическим аппаратом алгебры переключательных схем.

Булева алгебра

Булева алгебра основана Джорджем Булем (1815-1864 гг) и является с середины 30-х годов прошлого столетия основой для анализа цифровых логических схем. Булевой алгеброй называется непустое множество A с двумя бинарными операциями логического умножения 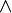(конъюнкция) и логического сложения 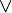(дизъюнкция), унарной операцией (отрицание) и двумя выделенными элементами: 0 (Ложь) и 1 (Истина). Основные равносильности Булевой алгебры представлены в табл.2.1. Использование следствий законов алгебры логики позволяет сократить (минимизировать) логические выражения.

Формальное описание работы схемы в виде Булева выражения позволяет построить логическую схему устройства, реализующего заданный алгоритм. Однако сложность минимизации, отсутствие наглядности и возможности контроля всех возможных вариантов реализации алгоритма привело к использованию таблиц истинности и карт Карно для формального описания работы комбинационных логических схем.

Таблица 2.1

Сводная таблица равносильностей Булевой алгебры

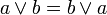
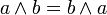
	коммутативность, переместительность
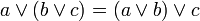
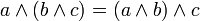
	ассоциативность, сочетательность
конъюнкция относительно дизъюнкции 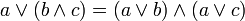дизъюнкция относительно конъюнкции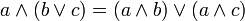	дистрибутивность, распределительность
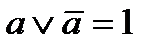
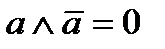
	комплементность, дополнительность (свойства отрицаний)
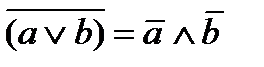
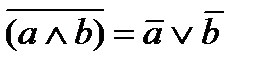
	законы де Моргана
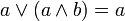
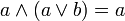
	законы поглощения (склеивания)
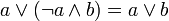
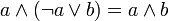
	Блейка-Порецкого
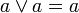
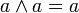
	идемпотентность
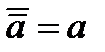
	инволютивность отрицания, закон снятия двойного отрицания
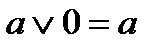
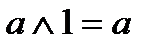
	свойства констант
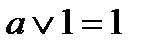
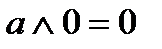
дополнение 0 есть 1 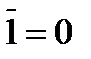дополнение 1 есть 0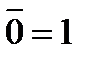
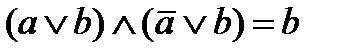
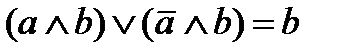
	склеивание

2.2 Использование таблиц истинности
для описания работы комбинационных логических схем

Таблицы истинности могут быть однозначно сопоставлены вербальным алгоритмам и приводившимся выше диаграммам. Если принадлежность произвольной точки прямоугольника множеству Y (или Z) считать «истиной» (с обозначением Т или 1), а противоположный случай – «ложью» (F или 0), то таблица истинности для операции И (конъюнкция) может быть изображена в виде табл. 2.2. Таблица истинности для операции ИЛИ (дизъюнкция) приведена в табл. 2.3.

Таблица 2.2 Таблица 2.3

Таблица истинности для операции И Таблица истинности для операции ИЛИ

В этих таблицах представлены четыре различные комбинации случаев принадлежности (или непринадлежности) точки множествам Y и Z.

Таблица истинности – наиболее полный формальный метод описания того, как работает логическая схема. Однако, описание работы схем с помощью таблиц истинности не только громоздко, но и, являясь первой ступенью синтеза любого цифрового устройства, не содержит описания его работы в минимальной форме, необходимой для облегчения анализа возможностей интегральных схем для конкретных приложений.

Для дальнейшего анализа и синтеза логической схемы необходимо преобразовать информацию в форме таблицы истинности в Булево выражение. Для записи в дизъюнктивно нормальной форме выделяются те комбинации переменных строки, которые дают логическую «1» на выходе. Аналогичным образом можно построить таблицу истинности по Булеву выражению.

Таблица истинности и Булево выражение по разному описывают принцип действия одной и той же логической схемы. Например, если имеется три датчика А, В и С, а включение электродвигателя или другого исполнительного устройства происходит при срабатывании датчиков В и С или датчика А, то формальное описание данного вербального условия работы можно представить в виде таблицы истинности для трех переменных (рис. 2.1), которому соответствует Булево выражение в нормально-дизъюнктивной форме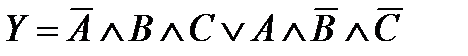

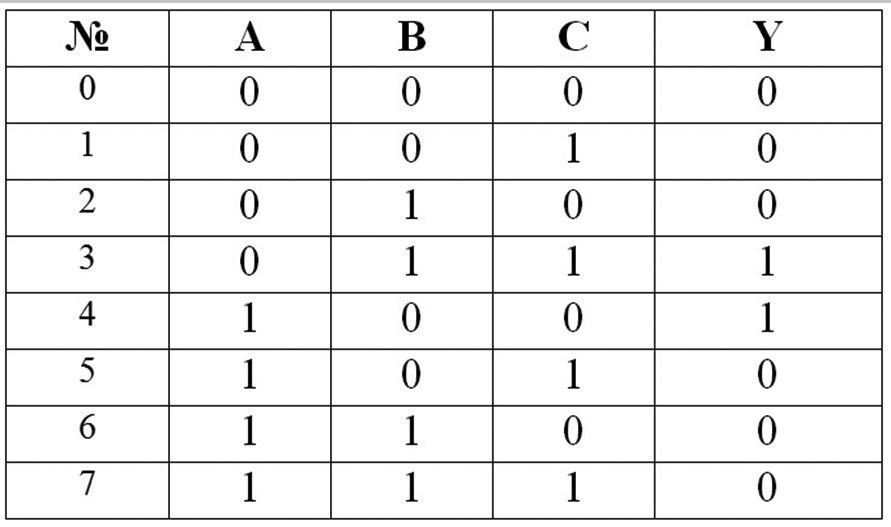
Рис.2.1. Таблица истинности для Булева выражения

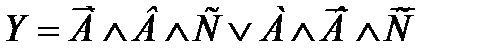
Необходимо учитывать все возможные комбинации входов, которые дают логическую единицу в таблице истинности. Например, минимизированное Булево выражение 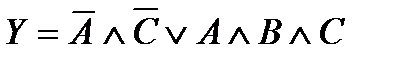дает не две, а три логических единицы для выходной функции Y в таблице истинности рис. 2.2.

Рис.2.2. Таблица истинности для Булева выражения

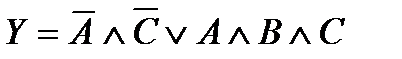
В другом примере требуется обеспечить управление исполнительным элементом Y так, чтобы он срабатывал при наличии сигналов от любых одного или двух из трех датчиков А, В, С. В данном случае формализация словесного алгоритма в виде таблицы истинности представлена на рис.2.3.

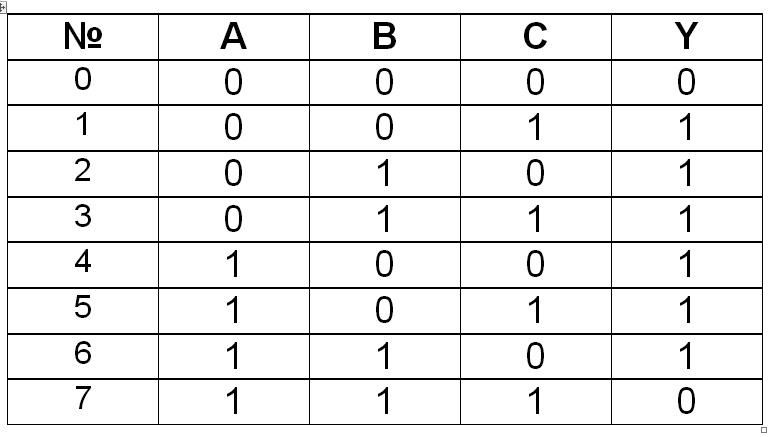
Рис.2.3. Формальное описание работы схемы по вербальному описанию
в виде таблицы истинности

Формальное описание в виде исходного Булева выражения в нормально-дизъюнктивной форме 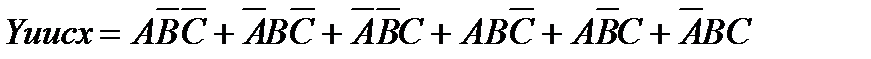. Логическая схема для реализации вербального алгоритма в соответствии с исходным Булевым выражением будет иметь вид (рис.2.4).

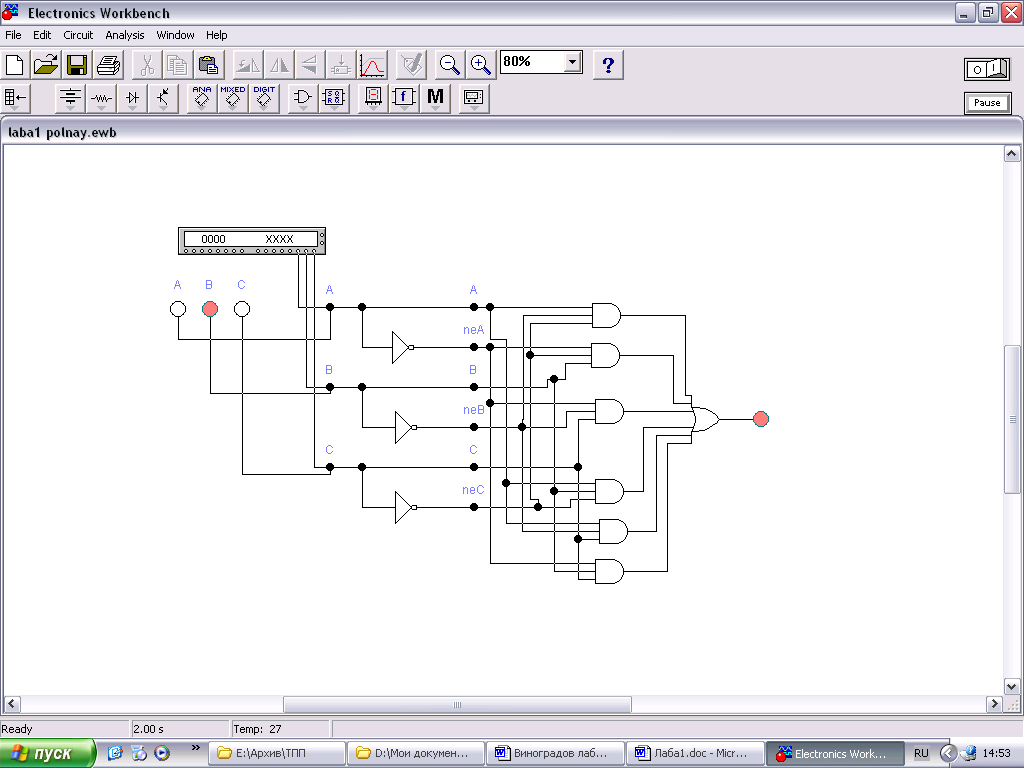
Рис.2.4. Исходная логическая схема для реализации вербального алгоритма

Используя равносильности Булевой алгебры можно минимизировать исходную функцию Y_исх ,

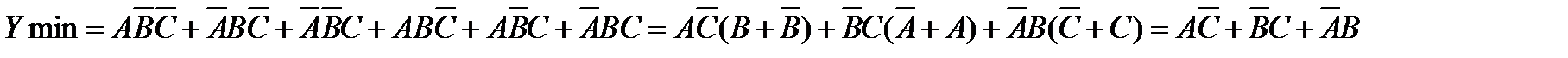
Логическая схема для реализации вербального алгоритма в соответствии с минимизированным Булевым выражением 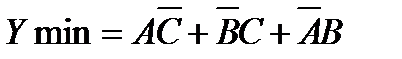будет иметь вид (рис.2.5). Минимизированная схема работает аналогично исходной, но при этом дешевле и имеет более высокую надежность.

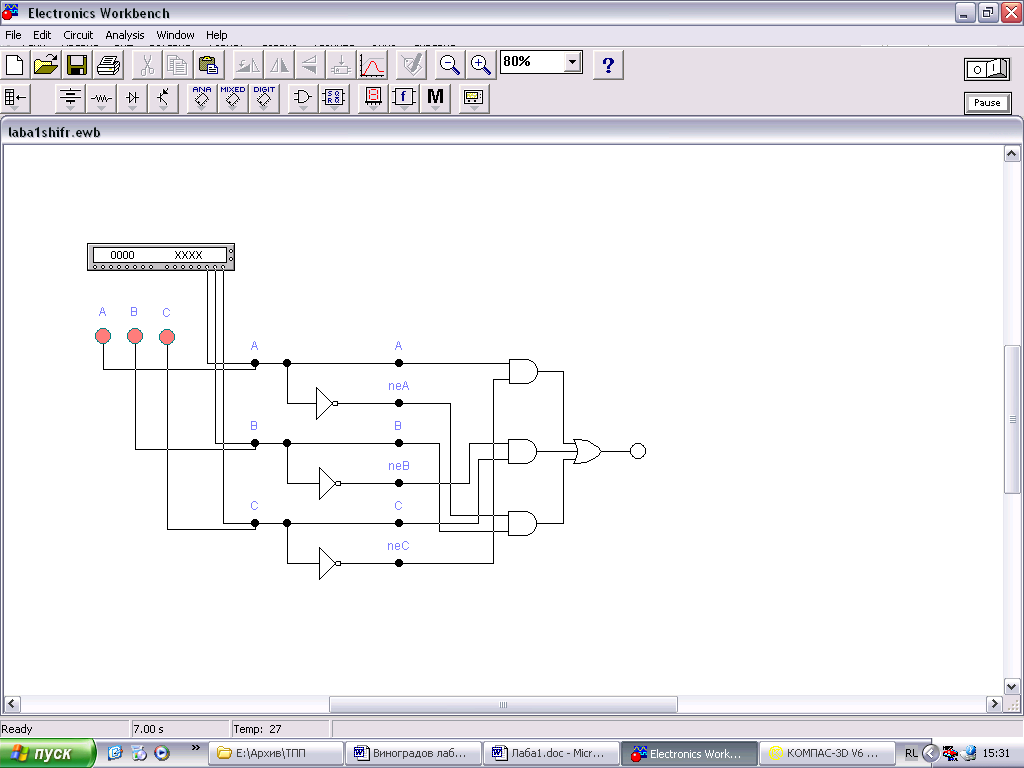
Рис.2.5. Минимизированная логическая схема для реализации вербального алгоритма

Если пронумеровать строки таблицы истинности в соответствии с десятичным значением соответствующих двоичных кодов, то можно записать условие работы схемы в виде набора номеров строк, где выходная функция принимает значение 1. Например, функция, записанная в виде Y=∑ (3, 5, 6, 9, 10, 12), может быть представлена соответствующей таблицей истинности (рис.2.6).

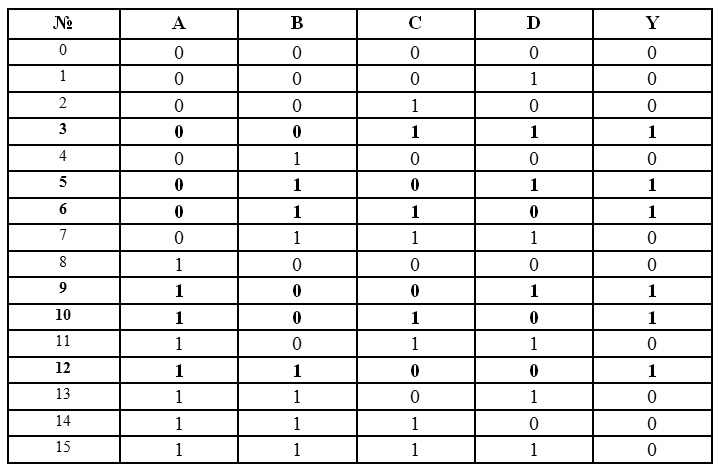
Рис.2.6. Таблица истинности

Формальное описание в виде исходного Булева выражения в нормально-дизъюнктивной форме будет иметь вид:

.

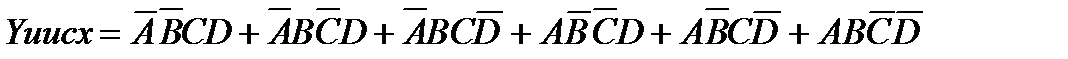Полученное Булево выражение может быть минимизировано с использованием свойств и аксиом Булевой алгебры и реализовано в виде логической схемы.

Преобразование входных величин с помощью карт Карно

Несмотря на то, что Булевы выражения и таблицы истинности используются для описания функционирования интегральных схем, ни один из этих способов изображения нельзя признать плодотворным при освоении современных методов логического конструирования. Карта Карно́ - графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного Булева куба. Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Другими словами в картах Карно при смещении на одну строку по вертикали или на один столбец по горизонтали изменяется лишь одна входная переменная за один шаг. Это исключает так называемые «гонки» или состязания, наблюдаемые при одновременном изменении двух и более входных переменных (рис.2.7).

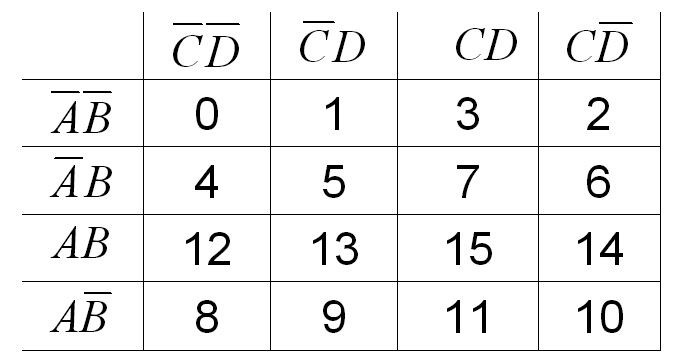
Рис.2.7. Соответствие номеров строк таблицы истинности и клеток Карты Карно

Таблица истинности для четырех входных переменных имеет 16 возможных комбинаций. На основании следствий алгебры логики упростить Булево выражение не просто. Карты Карно эту задачу значительно облегчают. Например, приведенное ниже исходное Булево выражение в дизъюнктивно нормальной форме можно представить в виде карты Карно, где очевидна возможность минимизации исходного Булева выражения путем объединения рядом стоящих единиц в группы по две и четыре (рис.2.8).

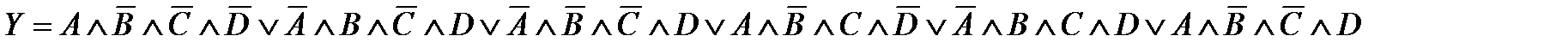
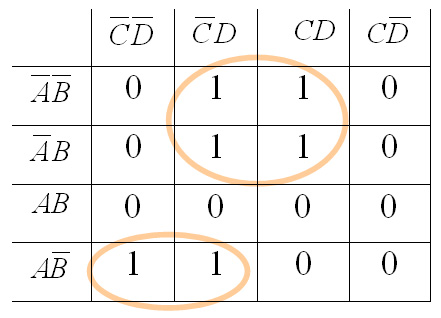
Рис.2.8. Матрица Карно

Шесть единиц нанесены на карту в соответствии шести членам в исходном Булевом выражении. Рядом стоящие единицы объединены в группы из 2^х и 4^х единиц. Члены, дополняющие друг друга внутри контура, исключаются. Объединив оставшиеся члены функцией ИЛИ, получим минимизированное выражение в дизъюнктивной нормальной форме (ДНФ) (сумма произведений). Количество групп, объединенных контурами определяет число членов минимизированного Булева выражения:

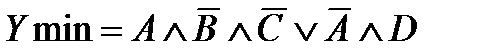
Таблица истинности (рис.2.9) для обоих вариантов одинаковая.

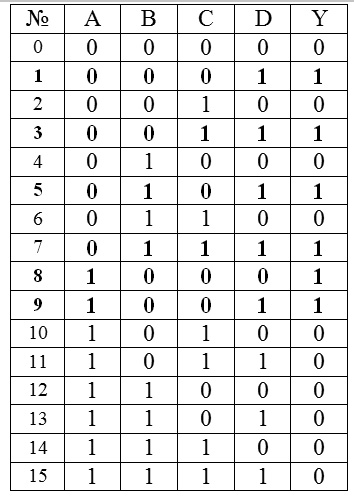
Рис.2.9. Таблица истинности для булева выражения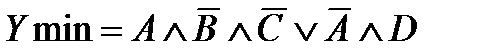

Логические схемы, составленные в соответствии с исходным и упрощенным выражением будут выполнять одинаковые логические функции, однако, количество элементов меньше, соответственно меньше стоимость, вес, объем, выше надежность.

Чем больше размеры объединяющих контуров, тем больше переменных можно опустить. Карту Карно можно как бы «свернуть» в цилиндр с вертикальной осью или с горизонтальной осью или образовать шар, объединяя угловые единицы. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности.

Карта Карно рассматривается как поверхность фигуры под названием тор. Единичному значению функции соответствуют p-клетки карты Карно. Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x₄, следовательно, они дают импликанту Х₁, Х₂, `Х₃. Две соседние импликанты первого ранга образуют импликанту второго ранга.

На карте Карно (рис.2.10) соседние клетки образуют две импликанты первого ранга и одну импликанту второго ранга. Минимизированное Булево выражение будет иметь вид

Y = Х₁, Х₂, `Х<sub>3</sub> + `Х₁, Х₂, Х₃+ `Х<sub>1</sub>, `Х₄

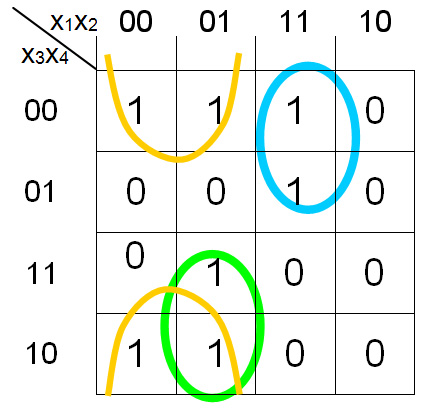
Рис.2.10.Карта Карно для четырех переменных

Если функция имеет 5 переменных, то рисуются две карты Карно: для x₅=0 и для x₅=1. Если 6 переменных - 4 карты так, чтобы в соседних картах соседние клетки имели одинаковые координаты (Рис.2.11).

Соседние p-клетки, соответствующие импликанте образуют компактную группу. Количество p-клеток в компактной группе является степенью двойки. Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.

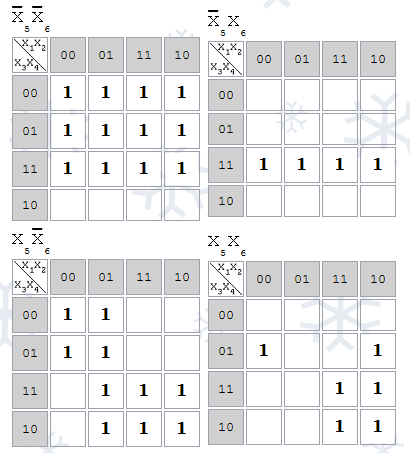
Рис.2.11. Варианты карт Карно

Если на картах Карно выделить все компактные группы наибольшей размерности, то получим минимизированное Булево выражение в дизъюнктивно-нормальной форме (ДНФ).

Минимизировать исходное Булево выражение и логическую схему (рис 2.4) гораздо удобнее с помощью карты Карно (Рис.2.12).

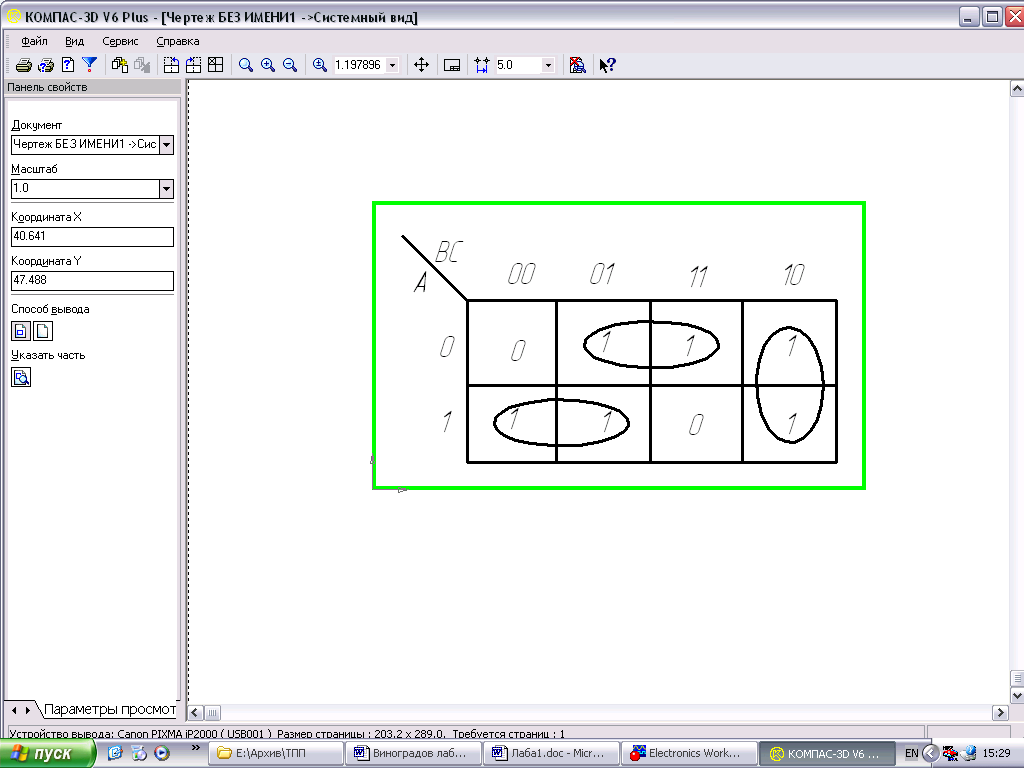
Рис.2.12. Карта Карно по таблице истинности (рис.2.3)

Нетрудно убедиться, что в результате выделения всех компактных групп наибольшей размерности получим минимизированное Булево выражение 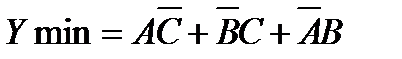, аналогичное полученному путем преобразования исходного Булева выражения. Однако, использование карт Карно нагляднее и во многих отношениях проще.

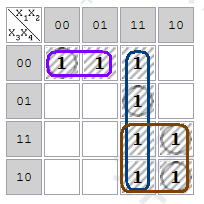
В качестве примера рассмотрим минимизацию функции 4-х переменных методом карт Карно, где две компактные группы размера 4 и одна компактная группа размера 2 (рис.2.13).

`

Рис.2.13. Пример карты Карно

Минимизированное Булево выражение в данном случае будет иметь вид

Y = `Х<sub>1</sub> Ù`Х₃ Ù`Х₄ Ú Х₁Ù Х₂ Ú Х₁, Ù Х₃