Компоновка узлов дискретных устройств

Компоновка – объединение узлов низшего уровня конструктивной иерархии в узлы следующего уровня: модулей – в ячейки, ячеек – в кассеты и т.д. При этом рассмотрим две постановки задачи: компоновку схем конструктивно унифицированными узлами без функциональной типизации; компоновку схем функционально типизированными узлами из заданного набора. Вторую задачу называют задачей покрытия или задачей компоновки типовых ячеек. Она обычно используется для компоновки элементов в ячейки, выпускаемые в виде больших интегральных схем. Это оправданно только при массовом производстве ячеек. Для обеспечения сбыта ячейки должны представлять собой некоторые функционально определенные узлы широкого применения. При выполнении ячеек в виде печатных плат (ТЭЗ) (типовых элементов замены) обычно используют первую постановку задачи, которую называют задачей компоновки конструктивных узлов. Рассмотрим для примера компоновку модулей в ячейки, хотя такие же алгоритмы могут быть использованы для компоновки ячеек в кассеты и кассет в шкафы.

Задачу компоновки конструктивных узлов можно представить как задачу оптимального разбиения множества элементов схемы (модулей) 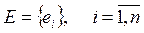на пересекающиеся подмножества 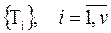при заданных ограничениях. Ограничения накладываются на число элементов 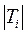и число внешних выводов g_i для подмножеств T_i :

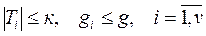
Т.н. «фиктивный элемент» e₀, отображающий разъем для подключения внешних выводов, из множества E исключается и образует свое подмножество Т_о. Связи других элементов с разъемом e₀ учитываются в процедуре формирования подмножеств. 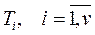. Подмножества T_i элементов размещаются на отдельных платах соответствующих ячеек. Соединения на платах – печатные проводники. Внешние выводы – разъемные. Соединения ячеек – проводным монтажом. Соединения ячеек сложнее (технологически), дороже, менее надежно. Поэтому одним из критериев оптимальности разбиения чаще всего служит минимум соединений между выделенными узлами (подмножествами T_i)_.

По аналогии с показателем связности r_ij элементов e_i и e_j при представлении схемы в виде взвешенного графа (ВГС) с матрицей R можно определить показатель 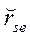связи между подмножествами T_s и T_e :

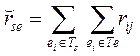, (6)

где r_ij – элемент матрицы R (ВГС).

Суммарный вес внешних связей узла (подмножества T_s) можно выразить:

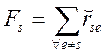, (7)

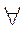– общности используется, чтобы наделить все предметные постоянные какой-либо общности общими свойствами.

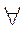Рх – для всех х выполняется...

а суммарный вес внешних связей между выделенными узлами

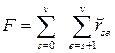. (8)

Требуется найти такое разрезание множества E на подмножества 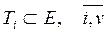, чтобы обеспечить минимум показателя F при соблюдении ограничений:

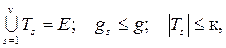
где g_s – число внешних выводов узла T_s.

Число возможных вариантов разрезания множества n элементов на v одинаковых подмножеств по к элементов в каждом составляет

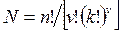(9)

При проектировании дискретных устройств n = 20 k = 5 N » 10¹⁰

В приведенной теоретико-множественной постановке задачу компоновки для отыскания оптимального решения можно свести к задаче целочисленного программирования. Т.к. даже при небольшом числе элементов (n = 15…20) задача имеет большую размерность, то практически применяют приближенные эвристические методы решения задачи оптимального разрезания множества элементов E на подмножества Ti. Точные методы используют иногда при небольших задачах для оценки приближения.

Все эвристические алгоритмы можно разбить на две группы: последовательные и итерационные.