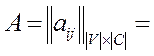Критерии оценки электронных схем
Для выполнения конструкторского проектирования используется исходная принципиальная или функциональная схема. Имеются несколько способов формализованного представления принципиальной схемы, отличающихся степенью подробности, необходимым объемом памяти ЭВМ, удобством использования в алгоритме проектирования.
Наиболее подробное описание схемы дает граф коммутационной схемы (ГКС)
ГКС = (E, C, V, A, B), (1)
где E – множество элементов 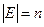 ; C – множество выводов
; C – множество выводов 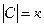 ; V –множество цепей (комплексов)
; V –множество цепей (комплексов) 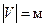 ; A – матрица связей между цепями и выводами; B – матрица связей между элементами и выводами.
; A – матрица связей между цепями и выводами; B – матрица связей между элементами и выводами.
Цепью (комплексом) называют совокупность эквипотенциальных точек в схеме.
Матрица А формируется по схеме следующим образом:
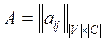 , (2)
, (2)
|
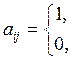
Каждая строка матрицы А соответствует определенной цепи, а каждый столбец – выводу. В матрице В строке соответствует элементу, а столбец – выводу:
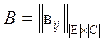 , (3)
, (3)
|
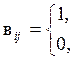
Матрицы А и В являются сильно разреженными. Информация, содержащаяся в ГКС (графе коммутационной схемы) для многих задач конструкторского проектирования избыточна. Чаще используют более компактное представление данных о проектируемой схеме в виде графа элементных комплексов (ГЭК):
ГЭК = (E,V,Q),
где E и V – множества элементов и цепей (комплексов); Q – матрица отношений между множествами:
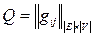 , (4)
, (4)
|
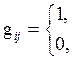
Граф элементных комплексов (ГЭК) может быть построен по ГКС (графу коммутации схемы). Для этого вычисляется Q=В´АТ, где АТ – транспонированная матрица А, умножение булевых матриц В и АТ выполняется по логической формуле
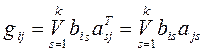 . (5)
. (5)
 Таким образом, в отличие от ГКС (графа коммутационной схемы) в ГЭК (граф элементных комплексов) рассматриваются только соединения элементов без указания конкретных выводов. Каждая цепь (комплекс) содержит множество эквипотенциальных точек. Граф монтажных соединений, в котором отображается порядок соединения этих точек, на первых этапах конструкторского проектирования не известен. Он строится на этапе трассировки соединений после решения задачи размещения и представляет собой дерево–связный граф без циклов. В то же время на этапах компоновки и размещения необходимо оценивать связность элементов между собой. Для такой оценки показателя связности rij элемента ei с элементом ej иногда используют число цепей, в которые входят оба элемента. Т.к. для соединения выводов одной цепи в действительности используются деревья соединений, оценка связности rij по числу цепей оказывается грубой. Поэтому используют вероятностные оценки, отражающие фактор неизвестности соединений в пределах комплекса. Пусть S-я цепь содержит ns выводов. Множество возможных соединений пар точек равно числу ребер в полном графе для ns вершин: 0,5ns (ns – 1). Дерево соединений ns вершин содержит ns –1 ребро. При этом математическое ожидание появления ребра полного графа при построении дерева S-й цепи будет рs=2/ ns .
Таким образом, в отличие от ГКС (графа коммутационной схемы) в ГЭК (граф элементных комплексов) рассматриваются только соединения элементов без указания конкретных выводов. Каждая цепь (комплекс) содержит множество эквипотенциальных точек. Граф монтажных соединений, в котором отображается порядок соединения этих точек, на первых этапах конструкторского проектирования не известен. Он строится на этапе трассировки соединений после решения задачи размещения и представляет собой дерево–связный граф без циклов. В то же время на этапах компоновки и размещения необходимо оценивать связность элементов между собой. Для такой оценки показателя связности rij элемента ei с элементом ej иногда используют число цепей, в которые входят оба элемента. Т.к. для соединения выводов одной цепи в действительности используются деревья соединений, оценка связности rij по числу цепей оказывается грубой. Поэтому используют вероятностные оценки, отражающие фактор неизвестности соединений в пределах комплекса. Пусть S-я цепь содержит ns выводов. Множество возможных соединений пар точек равно числу ребер в полном графе для ns вершин: 0,5ns (ns – 1). Дерево соединений ns вершин содержит ns –1 ребро. При этом математическое ожидание появления ребра полного графа при построении дерева S-й цепи будет рs=2/ ns .
Помимо вероятностного характера соединений между элементами, учитывают также различную важность цепей с помощью весовых коэффициентов 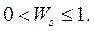 Так, например, с точки зрения помехоустойчивости цепи синхронизации являются более важными, чем цепи для передачи других сигналов. С учетом введенных понятий показатель связности двух элементов ei и ej можно оценить по формуле
Так, например, с точки зрения помехоустойчивости цепи синхронизации являются более важными, чем цепи для передачи других сигналов. С учетом введенных понятий показатель связности двух элементов ei и ej можно оценить по формуле
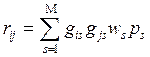 ,
,
где gis и gjs – элементы матрицы Q ГЭК (графа элементных комплексов); ps – вероятность появления ребра между элементами ei и ej в s-й цепи; 0<Ws£1 – весовой коэффициент важности цепи.
Величина rij может быть любым неотрицательным числом. Наиболее компактным формализованным представлением схемы, используемым при компоновке и размещении, является взвешенный граф схемы (ВГС):
ВГС = (E, R),
где E – множество элементов; R – матрица связности, элементы которой 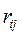 вычисляются по проведенной формуле и определяют взвешенную связность элементов ei и ej.
вычисляются по проведенной формуле и определяют взвешенную связность элементов ei и ej.
Матрица R симметричная и при большом числе элементов n – разреженная. Поэтому с целью экономии памяти ЭВМ взвешенный граф схемы удобно задавать списком, который можно отобразить двухмерным массивом Г [Д, 3]. Первая строка массива Г содержит номер 1й вершины e1 ВГС; наименьший номер вершины (i³2), связанной с e1 ребром; вес ребра. Вторая строка содержит номер первой вершины e1 ВГС; следующий по порядку номер вершины, связанный с e1 ребром, вес этой связи. Сначала описаны строки, соответствующие ребрам ВГС, инцидентным вершине 1, затем ребрам, инцидентным вершине 2 и вершинам, номер которых больше двух и т.д.
При формальных методах описания схем с помощью графов в качестве одного из элементов (е0) рассматривается разъем для подключения внешних выводов.
Пример:
Множество элементов E= 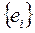 i=
i= 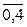
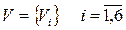 ;
; 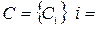
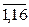
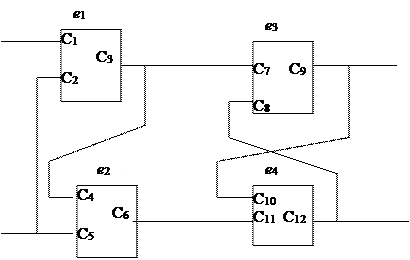
Дана схема
V1
V3 V5
C13 C15
V2
C14 C16
V4 V6
Рис. 13. Схема с обозначением элементов, выводов,
цепей для конструкторского проектирования
Обозначения элементов ei комплексов (цепей) Vi и выводов показаны на схеме. Для графа коммутационной схемы составим матрицы А и В согласно схеме соединений
| с/v | |||||||||||||||||
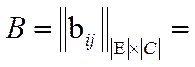 1 1
| C/E | |||||||||||||||
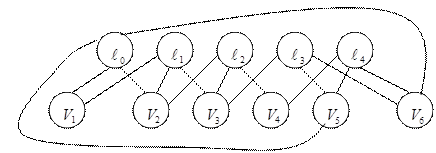
Рис. 14. ГЭК (граф элементных комплексов)
Граф содержит два множества вершин 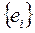 , i =
, i = 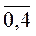 и
и 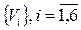 . Ребрами связаны вершины, принадлежащие разным множествам. Такой граф называют двудольным, отношения между вершинами графа описывает матрица
. Ребрами связаны вершины, принадлежащие разным множествам. Такой граф называют двудольным, отношения между вершинами графа описывает матрица
| s/i | ||||||
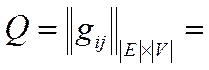 1 1
| ||||||
Вероятность Рs появления ребра полного графа при построении дерева s-й цепи, 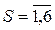 можно посчитать следующим образом:
можно посчитать следующим образом:
- в каждом столбце s матрицы Q подсчитываем число единиц ns: n1=n4=2; n2=n3=n5=n6=3;
- по формуле 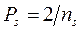 вычисляем вероятности: Р1=Р4=1; Р2=Р3=Р5=2/3;
вычисляем вероятности: Р1=Р4=1; Р2=Р3=Р5=2/3;
- полагая, что все цепи равнозначны 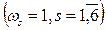 , определяем коэффициенты связности вершин
, определяем коэффициенты связности вершин
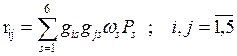
Значения 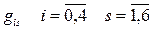 берутся из матрицы Q. После вычислений строим матрицу R взвешенного графа схемы:
берутся из матрицы Q. После вычислений строим матрицу R взвешенного графа схемы:
| Е/Е | |||||
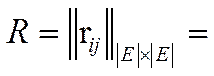 0 0
| 5/3 | 2/3 | 4/3 | 4/3 | |
| 5/3 | 4/3 | 2/3 | |||
| 2/3 | 4/3 | 2/3 | |||
| 4/3 | 2/3 | 2/3 | 4/3 | ||
| 4/3 | 4/3 |
Массив Г [9, 3], представляющий ВГС, будет иметь вид
Г [9,3] = 0, 1, 5/3, 0, 2, 2/3, 0, 3, 4/3, 0, 4, 4/3, 1, 2, 4/3, 1, 3, 2/3, 2, 3, 2/3, 2, 4, 1, 3, 4, 4/3
Число строк Д массива Г равно числу ненулевых элементов в матрице R выше главной диагонали
0 1 5/3
0 2 2/3
0 3 4/3
0 4 4/3
1 2 4/3
1 3 2/3
2 3 2/3
2 4 1
3 4 4/3
 |
5/3 2/3
4/3 4/3
4/3
2/3 1
2/3
4/3
Рис. 15. взвешенный граф схемы
Дата добавления: 2021-01-26; просмотров: 682;