Размещение элементов

Рассмотрим на примере размещения элементов на плате. Цель размещения – обеспечение удобства трассировки и уменьшение искажений сигналов. Искажения связаны с длиной соединений, зависящей от размещения. Критерий оптимального размещения:

- уменьшение суммарной длины F всех соединений;

- уменьшение длины наиболее длинного соединения;

- уменьшение числа пересечений соединений;

- максимум (максимизация) числа прямолинейных соединений (удобны для трассировки).

Исходные данные –плата (монтажное пространство) с заданными позициями 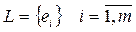для установки элементов (модулей), множество модулей 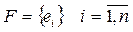n £ m с соответствующей схемой соединений. Связи задаются с помощью ГЭК (графа элементных комплексов) либо ВГС (взвешенным графо схемы). Расстояния между позициями e_i и e_j определяются одним из двух способов

1) ,

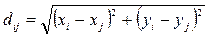2) ,

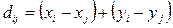где x_i, y_i, x_j, y_j – координаты позиций e_i и e_j,

1) по кратчайшему пути (проводные соединения);

2) параллельно осям (печатные платы).

Для заданного монтажного пространства построить матрицу расстояний между позициями 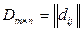. Размещение модулей в позициях монтажного пространства можно представить вектором

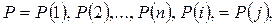
где P(i) – номер позиции, в которую будет помещен элемент e_i.

взвешенная для соединений между модулями e_i и e_j равна ,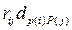

где 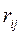– суммарный вес связей между модулями из матрицы R взвешенного графа схемы.

В задаче размещения могут быть заданы некоторые ограничения:

- поместить некоторый модуль или группу модулей в заранее определенные позиции;

- запретить некоторые позиции для размещения модулей.

Пусть A_s – множество закрепленных модулей с фиксированными заранее позициями. Суммарную взвешенную длину соединений модуля e_i с модулями 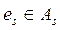можно представить в виде

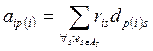
Суммарная взвешенная длина соединений F при некотором размещении Р будет

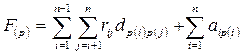
Число вариантов размещения равно числу перестановок n компонентов вектора P = (P(1), …, P(n)). Матрица назначений

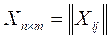, где

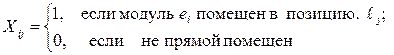
С использованием переменных X_ij задачу размещения можно представить в виде обобщенной задачи квадратичного назначения. Найти матрицу Х, для которой достигает минимума функционал

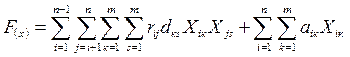
Для точного решения задачи квадратичного назначения требуются большие затраты машинного времени. Используются при небольшой размерности (m, n < 20).

Практическое применение находят эвристические алгоритмы, например последовательные алгоритмы размещения, с учетом суммарного веса связей каждого элемента с остальными. Первый элемент с максимальным показателем располагают в одну из центральных позиций, сумма расстояний от которой до остальных минимально

.

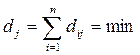Иногда в качестве начального выбирают закрепленный модуль – разъем.

При выборе очередного из неразмещенных модулей учитывается:

- Максимальная связь с одним из размещенных модулей r_i(E_к) суммарный вес связей со всеми размещенными модулями 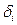и неразмещенными.

Обозначим: 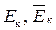– множества размещенных и неразмещенных модулей;

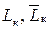– множество занятых и свободных позиций;

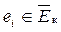– очередной модуль.

Для принятия решения используют следующие показатели:

;

,

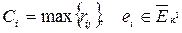
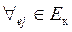
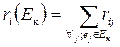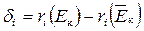где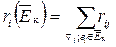

С_i –максимальная связь с одним из размещенных модулей; r_i(E_к) – суммарный вес связей со всеми размещенных модулями; 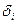– показатель, учитывающий связи как с размещенными, так и с неразмещенными модулями.

В качестве очередного модуля выбирается такой, у которого эти показатели максимальны. Для их определения используется матрица R ВГС.