Элементов на подмножества в задачах компоновки
Последовательные алгоритмы не требуют начального разделения множества Е. из исходного множества выделяется первое подмножество Т1. Затем из оставшегося множества выделяется второе подмножество Т2 и т.д., пока не произойдет полное разделение множества Е на подмножества Тi, 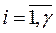 .
.
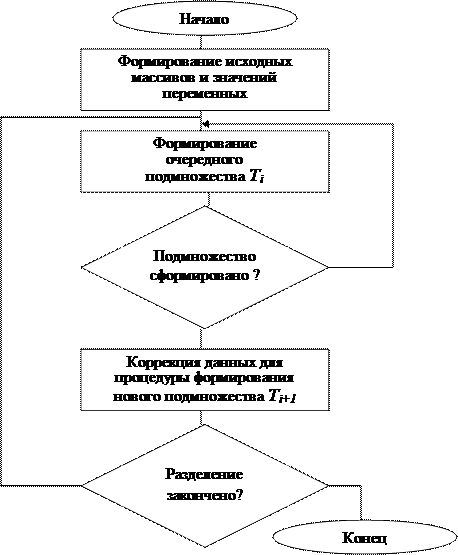
Обобщенная схема последовательного алгоритма показана на рис. 14.
Когда формируется очередное подмножество, важно определить способ выбора первого элемента и очередного элемента. Используются различные показатели для обоснованного принятия решений. В качестве данных используется граф элементных комплексов с матрицей Q и взвешенный граф схемы с матрицей R.
Возможны различные процедуры формирования подмножества Tt. В качестве примера рассмотрим метод максимальной конъюнкции и минимальной дизъюнкции. В нем используется матрица Q. Пусть А – множество нераспределенных элементов, 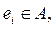 а В – некоторое подмножество А, не содержащее ei .Вводим показатели:
а В – некоторое подмножество А, не содержащее ei .Вводим показатели:
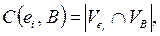 (10)
(10)
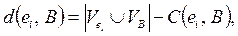 (11)
(11)
где 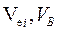 – множество цепей (комплексов), связанных с элементом ei и с элементами множества В соответственно.
– множество цепей (комплексов), связанных с элементом ei и с элементами множества В соответственно.
Показатель С (ei , В) определяет число цепей, соединяющих элемент ei иэлементы множества В, а показатель d(ei, В) – число цепей, которые не являются общими у ei и элементов из В. Для вычисления показателей С и d можно использовать операции над множествами, либо скалярные произведения векторов – строк Si матрицы Q. В этом (втором) случае
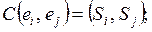 (12)
(12)
 |
Нет
Да
Нет Да
Рис. 16. Обобщенная схема последовательных алгоритмов разделения множества
элементов на подмножества в задачах компоновки
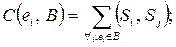 (13)
(13)
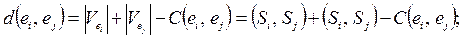 (14)
(14)
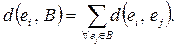 (15)
(15)
Вначале принимается A=E\e0. Процедура формирования подмножества Тi содержит четыре шага:
1. В качестве первого элемента из множества Е выбирается такой, который наибольшим числом цепей связан с внешними выводами схемы. С этой целью для всех 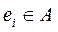 вычисляется показатель
вычисляется показатель 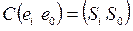 . Выбирается элемент es с наибольшим значением этого показателя. Если их несколько, то из них выбирается ej, у которого минимален показатель
. Выбирается элемент es с наибольшим значением этого показателя. Если их несколько, то из них выбирается ej, у которого минимален показатель 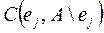 . Выбранный элемент включается в подмножество Тi и исключается из множества А.
. Выбранный элемент включается в подмножество Тi и исключается из множества А.
2. Пусть в подмножестве 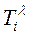 уже находится несколько элементов. На очередном шаге выбирается элемент,
уже находится несколько элементов. На очередном шаге выбирается элемент, 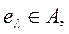 для которого значение
для которого значение 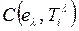 максимально. Если их несколько, то выбирается с наименьшим значением
максимально. Если их несколько, то выбирается с наименьшим значением 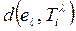 . Поэтому процедура и называется методом максимальной конъюнкции и минимальной дизъюнкции.
. Поэтому процедура и называется методом максимальной конъюнкции и минимальной дизъюнкции.
3. Перед назначением элемента 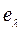 в подмножество
в подмножество 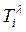 проверяется ограничение по числу внешних соединений gi для подмножества
проверяется ограничение по числу внешних соединений gi для подмножества 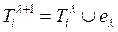 . Если ограничения соблюдаются, то элемент
. Если ограничения соблюдаются, то элемент 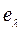 включается в подмножество
включается в подмножество 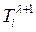 и исключается из множеств А. В противном случае в соответствии с п.2 выбирается другой кандидат для включения в
и исключается из множеств А. В противном случае в соответствии с п.2 выбирается другой кандидат для включения в 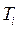 .
.
4. Процесс формирования подмножества 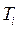 продолжается до тех пор, пока число элементов в нем не станет равным заданному числу К, либо пока при любом новом назначении элемента из А в
продолжается до тех пор, пока число элементов в нем не станет равным заданному числу К, либо пока при любом новом назначении элемента из А в 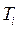 не станут нарушаться заданные ограничения или не будут распределены все элементы из А.
не станут нарушаться заданные ограничения или не будут распределены все элементы из А.
При наличии двух ограничений на число элементов К и на число внешних выводов g число V подмножеств 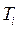 заранее неизвестно.
заранее неизвестно.
Допустимое число внешних выводов g в узлах, содержащих по К элементов, также заранее неизвестно. Часто имеется возможность изменять число g, выбирая различный тип разъема.В этом случае задачу разделения Е сначала решают без ограничений на число внешних выводов, затем по полученным подмножествам 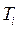 анализируют требуемые значения
анализируют требуемые значения 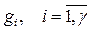
5.1. Процедура формирования подмножеств 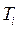 с использованием ВГС
с использованием ВГС
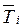 – множество элементов, (включая e0), не вошедших в подмножество
– множество элементов, (включая e0), не вошедших в подмножество 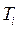 . Для элементов
. Для элементов 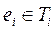 введем показатель
введем показатель 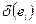 – коэффициент связности:
– коэффициент связности:
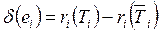 , (16)
, (16)
где 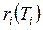 и
и 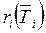 – суммарный все связей элемента ei c элементами из
– суммарный все связей элемента ei c элементами из 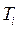 и
и 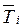 соответственно. Показатель
соответственно. Показатель 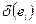 может быть как положительным, так и отрицательным. Пусть А – множество нераспределенных элементов. Сначала
может быть как положительным, так и отрицательным. Пусть А – множество нераспределенных элементов. Сначала
A=E\e0.
Процедура содержит три шага:
1. Первым элементом в формируемое подмножество 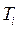 выберем такой ei, у которого значение rQi в матрице R максимально. Если их несколько, то из них выберем элемент ej с минимальным значением
выберем такой ei, у которого значение rQi в матрице R максимально. Если их несколько, то из них выберем элемент ej с минимальным значением 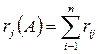 .
.
Этотэлемент помещается в 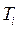 и исключается из А.
и исключается из А.
2. После того, как часть элементов помещена в формируемое подмножество 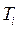 ,ищется элемент
,ищется элемент 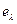 из А с максимальным коэффициентом связности
из А с максимальным коэффициентом связности 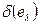 . Если их несколько, то выбирается с меньшим номером.
. Если их несколько, то выбирается с меньшим номером.
3. Формирование подмножества 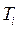 заканчивается, если число элементов в нем достигает заданного значения К либо А = Ø.
заканчивается, если число элементов в нем достигает заданного значения К либо А = Ø.
Иногда в п. 2 выбор элемента 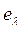 производят в два этапа: сначала выбираем элемент с максимальным значением
производят в два этапа: сначала выбираем элемент с максимальным значением 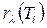 , а если их несколько, то из них – с минимальным значением
, а если их несколько, то из них – с минимальным значением 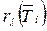 .
.
Очевидно, что при последовательных процедурах разделения первые подмножества содержат сильно связанные элементы, а последние – слабо связанные. Такой результат оптимальным можно назвать условно. Его можно улучшить, используя итерационные алгоритмы. При этом меняются местами элементы (или их группы), принадлежащие различным подмножествам с целью уменьшения суммарного веса связей между подмножествами. Чаще всего – парные перестановки, т.е. меняют местами два элемента. Для оценки эффективности перестановки рассматривают изменение суммарного веса связей между выделенными подмножествами до и после перестановки
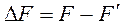 .
.
Сначала делаются попытки перестановок каждого из элементов 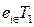 со всеми остальными элементами из
со всеми остальными элементами из 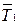 . Находится вариант с
. Находится вариант с 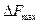 и эта перестановка выполняется, если
и эта перестановка выполняется, если 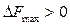 . Процедура многократно повторяется. Если все пробы перестановок имеют
. Процедура многократно повторяется. Если все пробы перестановок имеют 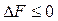 , то итерации перестановок элементов из Т1 заканчиваются. Затем берутся элементы из Т2 и осуществляются попытки перестановок с элементами из
, то итерации перестановок элементов из Т1 заканчиваются. Затем берутся элементы из Т2 и осуществляются попытки перестановок с элементами из 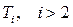 и т.д. При этом необходимо следить за изменением числа внешних выводов.
и т.д. При этом необходимо следить за изменением числа внешних выводов.
Для определения первого или очередного элемента, включаемого в формируемое подмножество Ti в последовательных алгоритмах, а также для выбора пары элементов очередной перестановки в итерационном алгоритме удобно использовать ВГС с матрицей R, учитывающей вероятностный характер соединений элементов в цепях (комплексах), эти операции требуют меньше машинного времени, объем ОЗУ, чем операции с элементами матрицы Q ГЭК. ГЭК необходим для определения числа внешних выводов формируемых подмножеств. Выполнение каждой перестановки требует К(n-к) проб, где К – число элементов в подмножестве, n – общее число элементов. Число итераций для экономии машинного времени можно ограничить.
Оптимум функции F(N) может быть в случае парных перестановок локальным, например

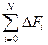
Глобальный оптимум



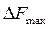 °
°
локальный


 ° ° ° N
° ° ° N

 °
°
0 1 2 3 4 5 6
°
Рис. 17. Оптимум функции F(N)
Использование многократного применения алгоритма парных перестановок, когда работа алгоритма не прекращается после снижения 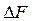 . N=1 – локальный оптимум, N=4 – глобальный оптимум. Нужна групповая перестановка с номерами 1,2,3,4.
. N=1 – локальный оптимум, N=4 – глобальный оптимум. Нужна групповая перестановка с номерами 1,2,3,4.
Дата добавления: 2021-01-26; просмотров: 578;











