Задачи трассировки соединений
Трассировка – наиболее трудоемкий этап конструкторского проектирования дискретных устройств. Исходными данными являются:
- список цепей;
- параметры коммутационного поля;
- параметры конструкции модулей;
- данные по их размещению.
Задача – выполнить оптимальную трассировку монтажных соединений для всех цепей.
Показатели качества трассировки:
- размеры п/п;
- суммарная длина соединений;
- число слоев проводящих покрытий;
- число межслойных переходов;
- число углов в соединениях.
Основные ограничения при трассировке – метрические, связанные с ограниченным объемом монтажного пространства и длиной трасс соединений. Для проводного монтажа ограничивается число проводников, подсоединяемых к одному контакту. Для печатных – отсутствие пересечений в одном слое.
Существующие алгоритмические методы трассировки можно разделить на 2 группы:
- топографические, учитывающие главным образом метрологический аспект задачи (длину соединений);
- графотеоретические, учитывающие главным образом топологический аспект (расположение соединений различных цепей без пересечений).
Последний метод используется для трассировки внутри модулей. Для трассировки в ячейках, блоках и шкафах – топографический метод.
Можно выделить следующую последовательность частных задач:
1. Определение очередности цепей при трассировке соединений.
2. Составление списка соединений (определение пар точек монтажного производства, которые требуется соединить).
3. Распределение соединений по слоям.
4. Определение очередности трассировки соединений.
5. Трассировка соединений.
В настоящее время наибольшее распространение получили последовательные алгоритмы трассировки, в которых цепи трассируются одна за другой, и все магистрали, занятые предыдущими цепями, считаются запрещенными для последующих. Существует «конкуренция» цепей в отношении магистралей вследствие неизбежного перекрытия участков монтажного пространства, занятых проводниками различных цепей.
Целью задачи определения очередности цепей при трассировке соединений является обеспечение для каждой цепи достаточного ресурса магистралей и при этом по возможности минимальное уменьшение ресурса для последующих цепей.
Пусть коммутационная схема задана графом ЭК с матрицей 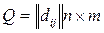 . Для каждой цепи Vi подсчитаем коэффициент связности
. Для каждой цепи Vi подсчитаем коэффициент связности
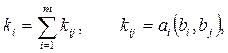
где ai – весовой коэффициент цепи Vi (в частном случае 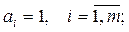 bi, bj – скалярное произведение векторов – столбцов матрицы Q.
bi, bj – скалярное произведение векторов – столбцов матрицы Q.
|

|
 4 4
4 4
|
|
|

|



|
|

 2 2
2 2
3 3
|
|
Проводной монтаж Печатный монтаж
Рис. 20. Дерево соединений для проводного монтажа (а) и для печатного монтажа (б)
Чем больше показатель ki, тем больше пересечений будет иметь цепь vi с другими цепями. Поэтому трассировку начинают с той цепи, которая имеет наибольшее значение показателя ki и далее рассматриваются цепи в порядке убывания значений этого показателя.
Для печатного проводника допускается ответвление от любой точки проводника.
При этом в дереве соединений появляются дополнительные вершины, не соответствующие выводам модулей
Такое дерево называют деревом Штейнера. Задача построения минимального дерева Штейнера сложнее, чем при построении дерева типа вывод – вывод.
Для ее решения существенно определить метрику – способ вычисления расстояния между двумя точками в монтажном пространстве. Наиболее часто используется ортогональная метрика, при которой расстояния определяются из выражения
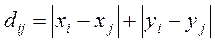
Дата добавления: 2021-01-26; просмотров: 548;











