Алгоритм парных перестановок

Последовательные алгоритмы дают неплохие результаты, но далекие от оптимального, поэтому их используют для начального размещения, затем улучшают с помощью итерационного алгоритма. Например, алгоритм парных перестановок. Пробы перестановок двух модулей, затем определяется относительное приращение суммарной взвешенной длины соединений F

.

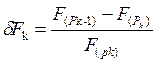Если 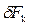больше некоторого положительного заданного значения, то перестановка выполняется, и алгоритм переходит к следующему шагу, пока не опробуются все пары.

Иногда после получения оптимального размещения трассировка соединений по кратчайшим путям оказывается невыполнимой. При решении задачи размещения следует учитывать требования последующей трассировки, т.е. решать задачи совместно.

При проектировании печатных плат позиции для установки модулей расположены в узлах правильной прямоугольной решетки. Прокладка печатных соединений допускается в двух взаимно перпендикулярных направлениях (ортогональная трассировка), причем в областях платы, вытянутых вдоль рядов позиций для установки элементов. Эти области называют вертикальными и горизонтальными каналами.

Пропускная способность канала отличается в зависимости от осей. Существует направление преимущественной трассировки. Максимальное число линейных цепей должно быть уложено в каналы этого преимущественного направления. Допустим, что наибольшую пропускную способность имеют вертикальные каналы. Очевидно, что в этом случае в одном столбце следует размещать, наиболее, сильно связанные модули. С учетом этого обстоятельства задача размещения модулей на плате разделяется на следующие подзадачи, решаемые последовательно:

1. Разделение множества модулей исходной схемы на минимально связанные подмножества, соответствующие столбцам позиций платы (задача разрезания).

2. Размещение модулей внутри подмножеств (в позициях столбцов) (задача линейного размещения).

3. Минимизация суммарной взвешенной длины межстолбцовых и межрядовых соединений.

В первой задаче используется сначала последовательный, а затем итерационный алгоритмы разрезания множества модулей E на подмножества.

Во второй задаче для каждого модуля некоторого столбца определяется строка. Формирование строк начинается с первой. Выясняются закрепленные модули. В оставшиеся позиции строки помещаются незакрепленные модули, причем все модули должны оставаться в своих столбцах.

В третьей задаче используется итерационный алгоритм парной перестановки столбцов, а затем строк. Запрещается переставлять столбцы и строки с закрепленными модулями. Все связи внутри объединенного модуля (столбца) игнорируются. Рассматриваются только связи между объединенными модулями. Аналогичное преобразование выполняется и при перестановках строк.

Хотя рассмотренный алгоритм и учитывает требование трассировки, связанное с неравномерной загрузкой каналов, в нем отсутствует минимизация числа магистралей в каналах, а размещение модулей в столбцах и строках проводится по критерию минимизации суммарной взвешенной длины соединений соответствующих групп модулей. При заданной ширине канала и полученном размещении модулей может оказаться невозможной трассировка соединений всех цепей по кратчайшим путям. Поэтому после размещения модулей по рассмотренному алгоритму надо оценить загрузку каналов и произвести коррекцию размещения перестановкой, чтобы уменьшить загрузку каналов.

При разработке печатных плат выбираются такие параметры как число позиций m для установки модулей, шаг установки модулей в горизонтальном и вертикальном направлениях h_x h_y , число внешних выводов g, число слоев для реализации соединений. Выбор осуществляется с учетом экономических, технологических, схемотехнических факторов; на основе опытных данных.

Необходимое число внешних выводов можно оценить по формуле

,

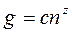где С – среднее число выводов на модуле; n – число модулей на плате; z – 0,57 …0,75. Большее значение z – операционным устройствам параллельного типа, меньшее – комбинационным логическим схемам.

Шаги установки модулей в горизонтальном и вертикальном направлении, выражаемые числом шагов между проводниками

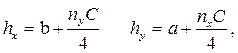
где n_x – число модулей в ряду (строке); n_y – число модулей в столбце; C – среднее число выводов в модуле; a и b – размеры модуля вдоль вертикальной и горизонтальной оси в шагах.

Удельная площадь платы (на один модуль)

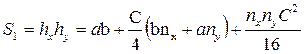
С увеличением числа модулей n_x n_y удельная площадь S, увеличивается. При заданном числе элементов площадь платы будет минимальной, если 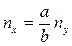. При этих условиях конфигурация платы приближается к квадрату.

Для решения задач распределения инвариантных контактов, помимо координат позиций для установки модулей в монтажном пространстве платы, необходимо определить пространственное положение каждого контакта модуля. Для каждого модуля вводится дополнительная прямоугольная система координат h, t, начало которой совмещается с позицией модуля дна плате x_i, y_i, а оси h, t, располагаются параллельно осям y и x платы. Для каждого типа модулей определяются координаты контактов и хранятся в памяти ЭВМ в соответствующих массивах. Это позволяет определять координаты любого контакта k_s модуля e_i в монтажном пространстве x_si = x_i + t_s; y_si = y_i + h_s , а также расстояние между контактами.

Распределение инвариантных контактов выполняется после размещения. Здесь выделяют две постановки задачи распределения контактов, использующие критерий минимизации длины соединений:

1. Распределение контактов при оптимизации внутреннего монтажа конструктивной единицы. Она (задача) используется для распределения контактов разъемов ячеек, блоков и т.д.

2. Распределение контактов при оптимизации внешнего монтажа по отношению к исследуемой конструктивной единице. Эта задача используется для распределения контактов модулей, перераспределения контактов ячеек и т.д.

На практике сначала распределяют контакты модулей, а затем контакты разъема.

Рассмотрим в качестве примера процедуру распределения контактов разъема. Контакты разъема 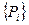находятся, как правило, на краю платы с одной стороны от контактов модулей 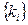, с которыми они должны быть соединены. Символы ЛК и ПК обозначают левый и правый канал для прокладки соединений с разъемом. Распределить контакты P_i следует так, чтобы не было пересечений.

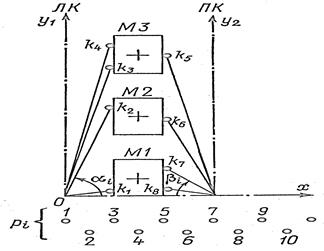
Рис. 18. Распределение контактов разъема: р₁₌k₄; р₂₌k_3; р_{3 =}k_2;р₄ = k₁;

р₅₌k₈; р₆₌k_7; р_{7 =}k_6;р₈= k₅

ОХ – проводим по нижней кромке М1; ОУ1 – перпендикулярно ОХ по оси каналу ЛК. Соединяем О (начало координат) с контактами, расположенными ближе к ЛК, чем к ПК (контакты k₁ … k₄). Упорядочение контактов k₁ – k₄ проводится по убыванию угла L_i . Контактам k₄, k₃, k₂, k₁ ставятся в соответствие контакты разъема P₁, P₂, P₃, P₄. Аналогично упорядочиваются контакты k₈…k₅, расположенные ближе к ПК по возрастанию угла 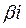. В этом случае соблюдается условие отсутствия пересечений и минимальная длина соединений внутри ячеек.

Обеспечение отсутствия пересечений проводников и минимальной длины соединений с точки зрения монтажа соединений между ячейками может оказаться неудачным. Т.к. чаще всего конструкция блока линейна, с размещением ячеек в ряд, наилучшим распределением контактов будет обеспечивающее параллельные соединения.

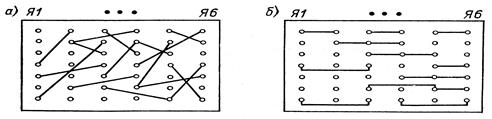
Рис. 19. Соединения между ячейками в блоке

при случайном распределении контактов разъема

по отношению к внешнему монтажу (а) и при оптимальном распределении (б)

Вначале распределяют контакты разъема первой ячейки с учетом внутреннего монтажа. Контакты разъема второй ячейки распределяются с учетом внутреннего монтажа, кроме тех, которые связаны с первой. Распределение выводов, связанных с первой ячейкой, производится с учетом распределения контактов разъема первой ячейки и им присваиваются те же номера контактов, что и в первой ячейке. Этим обеспечивается параллельность внешних соединений. Внутренний монтаж получается оптимальным для первой ячейки, но далек от оптимального для других. Поэтому такое распределение контактов разъема ячеек с учетом как внутреннего, так и внешнего монтажа, называют квазиоптимальным.