Умозаключения «от противного»
Схема умозаключения «от противного» такова: «Если из А следует В, то из не В следует не А». Другими словами, если верно АÞВ, то верно 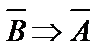 , и наоборот. Такое умозаключение лежит в основе рассуждения от противного и в математике. Если АÞВ назвать прямой теоремой, то ВÞА называется обратной теоремой, а
, и наоборот. Такое умозаключение лежит в основе рассуждения от противного и в математике. Если АÞВ назвать прямой теоремой, то ВÞА называется обратной теоремой, а 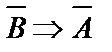 называется противоположной к обратной теореме.
называется противоположной к обратной теореме.
Покажем справедливость 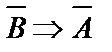 , при условии справедливости АÞВ. Нам нужно доказать, что если
, при условии справедливости АÞВ. Нам нужно доказать, что если 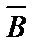 истинно, то
истинно, то 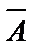 истинно. Другими словами, если В ложно, то А ложно. Но это очевидно, так как истинность А влечет за собой истинностьВ.
истинно. Другими словами, если В ложно, то А ложно. Но это очевидно, так как истинность А влечет за собой истинностьВ.
Приведем пример этого рассуждения из обыденной жизни. Допустим, что мы знаем, если дедушки нет дома, то засов на сарае стоит (АÞ В).Мы пришли и обнаружили, что засов на сарае не стоит ( 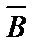 ). Значит, дедушка дома
). Значит, дедушка дома 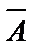 , т.е.
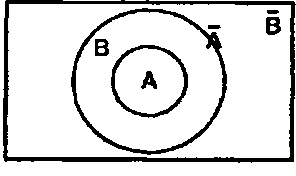
, т.е. 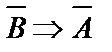 . Существует удобная иллюстрация приведенного умозаключения на диаграмме Эйлера-Венна. Если А ÌВ, то
. Существует удобная иллюстрация приведенного умозаключения на диаграмме Эйлера-Венна. Если А ÌВ, то 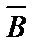 Ì
Ì 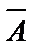 . На диаграмме это свойство хорошо видно:
. На диаграмме это свойство хорошо видно: 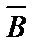 Ì
Ì 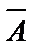
Кроме рассмотренных видов умозаключений, в логике изучают, много других видов умозаключений.
|
Дата добавления: 2021-01-26; просмотров: 588;











