ПРАКТИЧЕСКАЯ РАБОТА. МАТЕМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО
Цель. Раскрыть особенности, структуру и способы математических доказательств. Рассмотреть правила, в соответствии с которыми стояться правильные рассуждения необходимые для обучения младших школьников обосновывать суждения в курсе начальной математики.
Теоретическая часть
Вопросы к изучению
1. Понятие умозаключения
2. Дедуктивные умозаключения
3. Индуктивные умозаключения. Полная индукция
4. Неполная индукция
5. Математическая индукция
6. Аналогия
7. Умозаключения «от противного»
8. Некоторые виды неправильных умозаключений
Основные понятия темы
Ø умозаключение,
Ø посылка и заключение,
Ø дедуктивные (правильные) умозаключения,
Ø неполная индукция,
Ø аналогия,
Ø прямое доказательство,
Ø косвенное доказательство,
Ø полная индукция.
Неполная индукция и аналогия тесно связаны с дедукцией: выводы, полученные с помощью неполной индукции и аналогии, надо либо доказывать, либо опровергать. С другой стороны, дедукция не возникает на пустом месте, а является результатом предварительного индуктивного изучения материала.
Дедуктивные умозаключения позволяют из уже имеющегося знания получать новые истины, и притом с помощью рассуждения, без обращения к опыту, интуиции и т.д.
Математическое доказательство - это цепочка дедуктивных умозаключений, выполняемых по определенным правилам.
Практическая часть
1. Выскажите предположение, рассмотрев несколько частных случаев:
а) К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число?
б) Имеются два числа, ни одно из них не делится на 3. Может ли (и при каком условии), сумма этих чисел разделится на 3?
в) Верно ли, что квадрат четного числа есть число, кратное 4?
2. Даны верные равенства: 74 – 47 = 27; 52 – 25 = 27; 63 – 36 = 27. Верно ли, что разность любого двузначного числа и числа, записанного теми же цифрами, но в обратном порядке, равна 27?
3. Выяснив, что (12 + 4) : 2 = 12 : 2 + 4 : 2, ученик решил аналогично действовать при нахождении значения выражения (12 × 4) : 2, и записал: (12 × 4) : 2 = (12 : 2) × (12 : 4). Прав ли он?
4. Даны два утверждения: А (х) – «число х четное» и В (х) – «запись числа х оканчивается цифрой 4». Находятся ли они в отношении следования?
5. Почему следующее обобщение приводит к неправильному выводу: рассмотрим квадрат со стороной 1 см и измерим его углы. Все они равны 90°. Возьмем квадрат со стороной 2 см и тоже измерим все его углы. Они также получились равными 90°.Сделаем это 35 раз, предложив ученику проверить это самостоятельно. Вывод: все четырехугольники с равными сторонами имеют все углы по 90°?
6. Что играет роль отдельных подмножеств, на основании знаний о которых мы узнаем обо всем множестве в следующем умозаключении:
1 + 2 = 2 + 1; 1 + 3 = 3 + 1; 1 + 4 = 4 + 1; 1 + 5 = 5 + 1; 2 + 3 = 3 + 2;
2 + 4 = 4 + 2; 2 + 5 = 5 + 2; 3 + 4 = 4 + 3; 3 + 5 = 5 + 3; 4 + 5 = 5 + 4
Вывод. Сложение на множестве чисел {1, 2, 3, 4, 5} коммутативно.
7. Докажите, что если к произведению двух последовательных натуральных чисел прибавить большее из них, то получится квадрат большего числа.
8. Разность двух углов равна 10°. Докажите, что эти углы не могут быть вертикальными.
9. Докажите, что если х2 + 3х + 1 < 0, то х < 0.
10. Как изменится сумма двух чисел, если каждое слагаемое увеличить в три раза?
11. Каким числом может быть сумма двух нечетных чисел? Рассмотрите несколько частных случаев и выскажите предположение. Каким образом можно доказать его истинность?
12. Разделите каждое из чисел 32, 52 и 72 на 4. Чему в каждом из этих случаев равен остаток? Какое предположение можно высказать на основе полученных результатов? Сколько нечетных чисел нужно возвести в квадрат и разделить на 4, чтобы гарантировать истинность высказанного предположения?
13. Даны четыре последовательных нечетных числа. Верно ли, что произведение крайних чисел меньше произведения средних на 8?
14. Верно ли, что:
а) разность квадратов двух последовательных нечетных чисел делится на 8;
б) произведение двух последовательных четных чисел кратно 8;
в) разность между квадратом натурального числа, не делящегося на 3, и единицей делится на 3?
15. Покажите, что обосновывая решение следующих задач, младшие школьники могут использовать полную индукцию:
а) Дан ряд чисел: 3545, 3550, 3555, 3560, 3565. Можно ли утверждать, что каждое число этого ряда делится на 5?
б) Можно ли утверждать, что значения всех нижеприведенных выражений одинаковы: 326326:326; 236236:236; 626626:626.
в) Можно ли утверждать, что значения выражений в столбике одинаковы: 56:5; 7×8:(32:4); (65-9): (24:3)?
16. Закончите умозаключение так, чтобы оно было дедуктивным:
а) Если четырехугольник–прямоугольник, то в нем диагонали равны. Четырехугольник АВСD …
б) Равные треугольники имеют равные площади. Треугольники АВС и КLМ…
в) Для того чтобы ромб был квадратом, достаточно, чтобы в нем был прямой угол. Ромб АВСD…
17. Восстановите общую посылку в умозаключении:
а) Число 12 – натуральное, следовательно, оно положительное.
б) Число 15 – нечетное, следовательно, оно не делится на 2.
18. Постройте дедуктивное умозаключение, доказывающее, что 1) 130 делится на 10; 2) 137 не делится на 10; 3) Четырехугольник АВСD не является прямоугольником.
19. Докажите «от противного»:
1) что если в 10 коробках 21 елочная игрушка, то хотя бы в одной коробке лежит не менее трех елочных игрушек;
2) что множество А / (А Ç В) не пересекается с множеством В\ (А Ç В);
3) что, если а+3>10, то а ¹ 7;
4) что, если х2 – четное число, то х – четно;
5) что, если отрезок, проведенный через середину одной стороны треугольника до пересечения с другой стороной, равен половине длины третьей стороны, то этот отрезок есть средняя линия треугольника.
20. Докажите, что значение выражения (х–4)(2х+1) будет целое число, если х принимает значения –1, 0, 1, 4.
21. Доказать, что каждое составное натуральное число, большее 4, но меньшее 20, представимо в виде суммы двух простых чисел.
22. Докажите, что для простого р выражение р2+2 принимает только один раз значение простого числа.
23. Докажите методом математической индукции, что
а) 1+3+5+…+(2п–1)=п2; б) 1+3+6+…+ 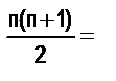
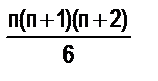 ;
;
в)12+22+32+…+п2 = 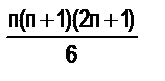 ; г) 13+23+33 +…+п3 =
; г) 13+23+33 +…+п3 = 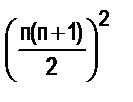 .
.
Дата добавления: 2021-01-26; просмотров: 961;











