ПРАКТИЧЕСКАЯ РАБОТА. СТРУКТУРА ТЕОРЕМЫ. ВИДЫ ТЕОРЕМ

Цель. Уметь раскрыть структуру теоремы, сформулировать на основании прямой теоремы обратную, противоположную и обратно противоположную теоремы.

Теоретическая часть

Вопросы к изучению

1. Структура теоремы.

2. Отличие теоремы от правила.

3. Виды теорем.

Основные понятия темы

Ø отношение логического следования между предложениями;

Ø отношение равносильности между предложениями;

Ø логическая структура тео­ремы и теорем, обратной, противоположной и обратно противопо­ложной данной.

Основные выводы

Ø Различные виды теорем связаны законом контрапозиции

(А Þ В) Û ( 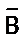Þ ).

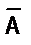Ø Теорема отличается от правила.

Обозначения

А Þ В – логическая структура теоремы, где А и В – высказывательные формы с одной или несколькими переменными. Предложение А – условие теоремы, В – ее заключение.

Практическая часть

Обязательные задания

1. Выделите условие и заключение в каждой из следующих теорем:

а) Если углы смежные, то их сумма равна 180°.

б) Диагонали ромба взаимно перпендикулярны.

в) Равенство треугольников есть достаточное условие их равновеликости.

г) Четность суммы есть необходимое условие четности каждого слагаемого.

2. Сформулируйте предложения, обратные следующим теоремам. Какие из них являются теоремами?

а) Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны.

б) Если параллелограмм является ромбом, то его диагонали взаимно перпендикулярны.

в) Если каждое слагаемое является четным числом, то и сумма четное число.

3. Сформулируйте предложения, противоположные теоремам, приведенным в предыдущем упражнении. Какие из этих предложений - теоремы?

4. Для каждой теоремы из упражнения 2 сформулируйте теорему равносильную ей согласно закону контрапозиции.

5. Для каждой из следующих теорем сформулируйте обратное, противоположное и обратно противоположное утверждения и установите, какие из них будут теоремами:

а) Если прямоугольник является квадратом, то его диагонали взаимно перпендикулярны и делят углы пополам.

б) Всякий параллелограмм с равными диагоналями есть прямоугольник или квадрат.

Творческие задания

1. Пользуясь законом контрапозиции, докажите следующие теоремы: а) Если p × q - нечетное число, то p и q нечетны (p, q Î N ); б) Если t² + n² ¹ 0, то t ¹ 0 или n ¹ 0.

2. Покажите, что следующие теоремы являются конъюнкцией двух теорем: а) На 5 делятся те и только те числа, запись которых оканчивается цифрой 0 или цифрой 5. б) Две прямые плоскости параллельны тогда и только тогда, когда они перпендикулярны одной и той же прямой. в) Для того чтобы в прямоугольном треугольнике катет составлял половину гипотенузы, необходимо и достаточно, чтобы угол лежащий против этого катета, был равен 30°.

3. Нижеприведенные правила взяты из учебников для начальных классов. Установите, какие теоремы сформулированы в виде этих правил: а) Если к разности прибавить вычитаемое, то получится уменьшаемое. б) Если произведение двух чисел разделить на один из множителей, то получим другой множитель. в) При делении любого числа на единицу в частном получится то число, которое делили.