Отношения равносильности между предложениями

<33 34 353637 38 39 >

Рассмотрим две высказывательные формы А(х) - «число делится на 3» и В(х) - «сумма цифр в записи числа делится на 3». Из школьного курса математики известно, что если число делится на 3, то сумма цифр в записи этого числа разделится на 3, и наоборот. В этом случае говорят, что предложения А(х) и В(х) равносильны.

Определение. Предложения А(х) и В(х) равносильны, если из предложения А(х) следует предложение В(х), а из предложения В(х) следует предложение А (х).

Для обозначения отношения равносильности используется знак Û. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) Û В(х), прочитать которое можно по-разному:

1) А(х) равносильно В(х).

2) А(х) тогда и только тогда, когда В(х).

3) А(х) - необходимое и достаточное условие для В(х).

4) В(х) - необходимое и достаточное условие для А(х).

Например, утверждение о том, что предложение «число делится на 3» и «сумма цифр в записи числа делится на 3» равносильны, можно сформулировать еще так:

- Число делится на 3 тогда и только тогда, когда сумма цифр вегозаписи делится на 3.

- Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.

Замечание. С теоретико-множественной точки зрения высказывание А(х) Û В(х) означает, что если Т_А - множество истинности высказывательной формы А(х), а Т_В - множество истинности высказывательной формы В(х), то Т_А = Т_В .

Задача 4. Доказать, что уравнения 3х (х - 2) = 0 и 3х(х - 2)(х + 3) = 0 равносильны на множестве целых неотрицательных чисел.

Решение. Множество решений первого уравнения –Т₁= {0, 2}, множество решений второго, заданного на множестве целых неотрицательных чисел, Т₂ = {0, 2}. Число -3 (см. задачу 3) множеству Т₂, не принадлежит, потому что оно не является целым неотрицательным. Имеем, что Т₁ = Т₂, следовательно, данные уравнения на множестве целых неотрицательных чисел равносильны.

Заметим, что мы рассматриваем понятия логического следования и равносильности для одноместных высказывательных форм. Для предложений, содержащих две и более переменных, эти понятия определяются аналогично.

Отметим также, что знак Û использовался раньше, в частности, при рассмотрении логической структуру явных определений понятий. Было установлено, что ее можно представить в виде а Û в. Употребление знака Û здесь не случайно. Дело в том, что определение, как говорят в математике, порождает два равносильных предложения, которые затем используются наряду с другими в доказательствах. Например, определение «квадратом называется прямоугольник, имеющий равные соседние стороны» порождает равносильные предложения: «если прямоугольник является квадратом, то в нем соседние стороны равны» и «если в прямоугольнике соседние стороны равны, то прямоугольник является квадратом». Использовать в доказательствах можно любое из этих двух.

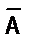Знак Ûтакже использовался в записи правил построения отрицания высказываний. Например, Û Ú 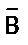; . В этом случае речь идет о равносильности высказываний определенной формы. При этом считают, что предложения равносильны, если они одновременно истинны, либо одновременно ложны. Другими словами, если их значения истинности совпадают при одинаковых наборах значений высказываний А и В.

<33 34 353637 38 39 >

Дата добавления: 2021-01-26; просмотров: 419;