ПРАКТИЧЕСКАЯ РАБОТА. ОТНОШЕНИЯ СЛЕДОВАНИЯ И РАВНОСИЛЬНОСТИ МЕЖДУ ПРЕДЛОЖЕНИЯМИ

Цель. Уметь устанавливать отношения следования и равносильности между парами предложений, видеть связь с начальным курсом математики.

Теоретическая часть

Вопросы к изучению

1. Отношения следования между предложениями.

2. Отношения равносильности между предложениями.

Основные понятия темы

Ø отношение логического следования между предложениями;

Ø отношение равносильности между предложениями.

Обозначения

Þ – логическое следование;

Û - равносильность.

Практическая часть

Обязательные задания

1. Следует ли предложение В(х) - «Число х четное» из предложения А (х), если: а) А(х) - «Число х делится на 6»; б) А(х) - «Число х делится на 7»; в) А(х) - «Число х делится на 2». Предложения А(х) и В(х) заданы на множестве натуральных чисел.

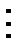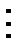2. Установите, находятся ли данные пары предложений в отношении следования: а) Треугольник АВС - равносторонний. Треугольник АВС– равнобедренный; б) Четырехугольник АВСD - квадрат. Четырехугольник АВСD – ромб; в) х 3 и х 6; г) а>2 и а>5.

3. Полученные в упражнении 2 утверждения о следовании сформулируйте шестью различными способами.

4. Сформулируйте следующие высказывания в виде «если ..., то ...»:

а) А - достаточное условие для В;

б) А - необходимое условие для В;

в) В -достаточное условие для А;

г) В - необходимое условие для А.

5. Среди следующих предложений укажите истинные; ответы обоснуйте:

а) Число а - натуральное, следовательно, и 15а - натуральное число.

б) Число 15а - натуральное, следовательно, а - натуральное число.

в) Если в четырехугольнике все углы прямые, то этот четырехугольник - прямоугольник.

г) Если в четырехугольнике диагонали равны, то этот четырехугольник - прямоугольник.

д) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы все его углы были равны.

е) Для того чтобы четырехугольник был прямоугольником, необходимо, чтобы все его углы были равны.

6. Для ложных высказываний из упражнения 5 постройте различными способами отрицание.

7. Равносильны ли следующие предложения А (х) и В(х), если: а) А(х) - «число делится на 9», В(х) - «сумма цифр в записи числа делится на 9»; б) А(х) - «каждое слагаемое суммы делится на 4», В(х) - «сумма делится на 4».

8. Какие из следующих предложений можно переформулировать, употребив слова «необходимо» либо «достаточно»: а) Если в четырехугольнике все углы равны, то четырехугольник является прямоугольником; б) Сумма двух четных чисел есть число четное; в) Всякое число, которое делится на 3 и на 5, делится на 15.

9. Какие из нижеприведенных высказываний истинные:

а) Для того, чтобы число делилось на 3, достаточно, чтобы оно делилось на 6.

б) Для того чтобы число делилось на 3, необходимо, чтобы оно делилось на 6.

в) Для того чтобы число делилось на 100, необходимо и достаточно, чтобы оно делилось на 10.

г) Для того чтобы число делилось на 10, необходимо и достаточно, чтобы оно делилось на 2 и на 5.

10. Вместо многоточия вставьте слова «необходимо» либо «достаточно», либо «необходимо и достаточно», чтобы данные предложения были истинными:

а) Для того чтобы сумма двух натуральных чисел делилась на 2, …, чтобы каждое слагаемое делилось на 2.

б) Для того чтобы каждое слагаемое делилось на 2, ... , чтобы сумма этих слагаемых делилась на 2.

в) Для того чтобы число делилось на 45, ... , чтобы оно делилось на 5 и на 9.

г) Для того чтобы угол был острым, ... , чтобы он был меньше прямого.

Творческие задания

1. Докажите, что предложение «в прямоугольнике Р диагонали взаимно перпендикулярны» и «прямоугольник Р - квадрат» равносильны. Утверждения о равносильности сформулируйте тремя различными способами.

2. Вставьте слова «и» либо «или» так, чтобы следующие высказывания были истинными: а) а × в =0 Û а =0 …в=0; б) а × в¹ 0 Û а¹ 0 …в¹ 0; в) х Î A В Û х Î А х Î В; г) хÏ А В Û х Ï А х Ï B.

3. В начальном курсе математики синонимом слова «необходимо» является слово «нужно» («надо»), и синонимом слова «достаточно» - слово «можно». Зная это, вставьте вместо многоточия слова: «нужно» либо «можно», так чтобы высказывания были истинными; ответы обоснуйте: а) Для того чтобы умножить сумму натуральных чисел на 5, … каждое слагаемое умножить на 5; б) Для того чтобы найти неизвестное слагаемое, ... из суммы вычесть другое слагаемое; в) Для того чтобы вычесть число из суммы, ... вычесть его из одного из слагаемых; г) Для того чтобы число было четным, ... чтобы оно делилось на 2.