ОШИБКА ОЦЕНКИ ДОЛИ КАЧЕСТВЕННОГО ПРИЗНАКА

Оценивать долю качественного признака мы теперь умеем: для этого вычисляем по выборке частоту.

Но для полноты ответа надо указать, какова погрешность нашего результата, иными словами: насколько велико отклонение полученной оценки доли качественного признака от неизвестного истинного значения?

Для ответа на этот вопрос необходимо вычислить дисперсию оценки доли качественного признака.

Мы с вами знаем общую формулу для дисперсии. Если подставить в неё все величины и произвести необходимые достаточно громоздкие математические преобразования (мы этого делать не будем), то она упрощается и принимает следующий вид:

.

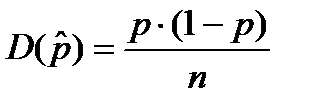n – это, по-прежнему, объём выборки.

p – доля качественного признака в генеральной совокупности.

В числителе стоит дисперсия двузначной случайной величины, описывающей качественный признак, поэтому

.

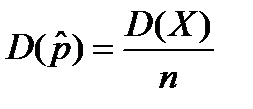Глядя на последнее равенство, можно сделать следующие выводы.

Дисперсия оценки доли качественного признака:

1) прямо пропорциональна дисперсии двузначной случайной величины;

2) обратно пропорциональна объему выборки.

Эти выводы справедливы и для оценки количественного признака, который мы рассмотрим чуть позже.

Итак, мы получили выражение для дисперсии оценки, но в него входит неизвестная величина: оцениваемая доля качественного признака. Следовательно, дисперсию оценки мы вычислить не можем.

Однако здесь можно применить одну «хитрость».

Если вместо неизвестной доли качественного признака подставить её оценку 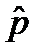, полученную по выборке, то мы получим приближённое значение дисперсии оценки доли качественного признака, т.е. выборочную дисперсию оценки:

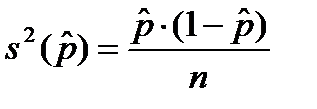
Для определения выборочной среднеквадратической ошибки извлекаем квадратный корень.

.

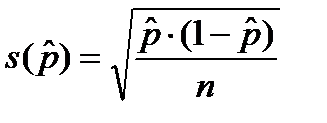Теперь, когда получено выражение для ошибки 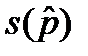, может записать полный ответ для задачи об оценке доли качественного признака в соответствии с требованиями статистики:

«Доля качественного признака равна оценка плюс-минус среднеквадратическая ошибка оценки

p = ± »

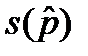Рассмотрим задачу, полностью совпадающую с домашним заданием.

Допустим, проводится криминологическое исследование такого уголовно-наказуемого деяния, как хулиганство. Известно, что в большинстве случаев хулиганство совершается в состоянии алкогольного опьянения.

Требуется оценить какова доля случаев, когда лицо, совершающее хулиганство, находится в состоянии алкогольного опьянения.

Для ответа на поставленный вопрос отбирается 49 уголовных дел по хулиганству:

n = 49 .

Предположим, в 40 из них зафиксировано нетрезвое состояние лица, обвиняемого в хулиганстве:

m = 40 .

Качественный признак в этой задаче – состояние алкогольного опьянения.

Вычислим оценку доли этого качественного признака

.

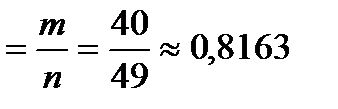Есть соблазн округлить до 0,8, но это преждевременно, т.к., отбрасывая значащие цифры, мы внесём дополнительную ошибку. Округлять можно только в ответе.

Итак, мы можем утверждать, что неизвестное значение доли качественного признака приблизительно равно её оценке.

p » 0,8163

Для того чтобы получить представление о степени приближенности сделанной оценки надо вначале вычислить выборочную дисперсию оценки.

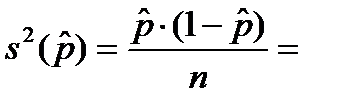
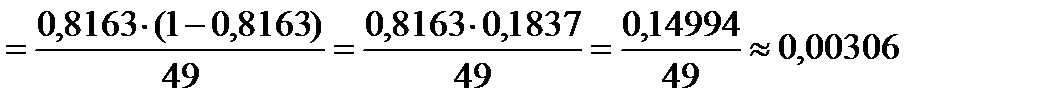
Единица измерения полученного значения – доля от целого в квадрате.

Теперь вычисляем выборочную среднеквадратическую ошибку оценки.

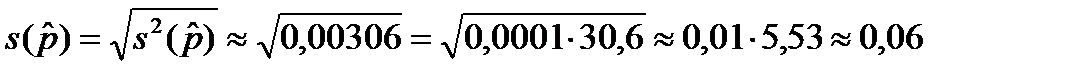
Теперь о том, сколько цифр оставлять в ответе.

По правилам округления в приближённых вычислениях ошибка округляется в ответе до единственной значащей цифры.

Для оцениваемого значения – правило другое: количество значащих цифр после запятой должно быть таким же, как и у ошибки. Или, другими словами, младший разряд оценки должен соответствовать разряду значащей цифры ошибки.

Единица измерения полученного значения – доля от целого.

Таким образом, ответ на поставленный вопрос таков: доля лиц, совершающих хулиганские действия в состоянии опьянения, составляет

p = 0,82 ± 0,06 .