Количественный признак – это показатель каждой единицы генеральной совокупности, выражающий ее определенное свойство числом и единицей измерения.

Например,

– стоимость ущерба в рублях,

– масса единицы товара в килограммах,

– численность преступной группы в человеках.

Количественный признак в генеральной совокупности характеризуется своим математическим ожиданием M(X), дисперсией D(X), а также распределением.

Оценка математического ожидания производится по формуле выборочного среднего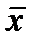

= = ,

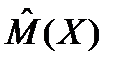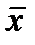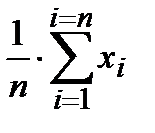а оценка дисперсии – по формуле выборочной дисперсии s²

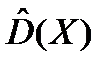= s² = .

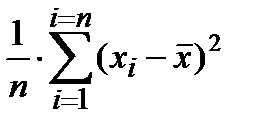Ошибка оценки математического ожидания зависит от дисперсии количественного признака в генеральной совокупности D(X) и уменьшается с ростом объёма выборки n. Выражение для дисперсии оценки математического ожидания количественного признака по выборке, как вывели математики, таково:

D( ) = .

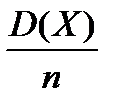Таким образом, дисперсия оценки математического ожидания количественного признака зависит

1) от дисперсии самого количественного признака

2) и от объема выборки.

Вычислить точное значение дисперсии оценки математического ожидания мы не можем, потому что нам неизвестна дисперсия генеральной совокупности.

Но мы сможем «схитрить» и вычислить приближённое значение дисперсии оценки математического ожидания, если в предыдущей формуле заменим неизвестную дисперсии генеральной совокупности D(X) на её оценку s², полученную по выборочным данным:

= .

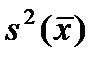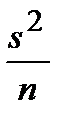Для определения среднеквадратической ошибки оценки математического ожидания необходимо извлечь из выборочной дисперсии квадратный корень:

= .

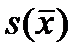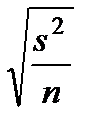Теперь, когда получено выражение для ошибки 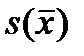, может записать полный ответ для задачи об оценке математического ожидания количественного признака в соответствии с требованиями статистики:

«Математическое ожидание равно оценка плюс-минус среднеквадратическая ошибка оценки

»

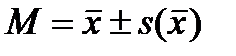Не следует путать по смыслу среднеквадратическую ошибку оценки математического ожидания 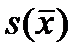и выборочное среднеквадратическое отклонение количественного признака s .

С увеличением объёма выборки 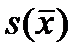стремится к нулю

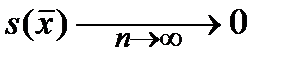
А s с увеличением объёма выборки – к среднеквадратическому отклонению генеральной совокупности s

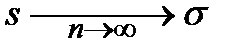
Для того чтобы почувствовать, насколько быстро убывает среднеквадратическая ошибка с ростом объёма выборки, построим две зависимости.

1) y =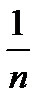

2) y =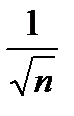

Мы видим, что с ростом n ошибка убывает, но не очень быстро.

0 1 2 3 4 5 6 7 8 9 n

0,5

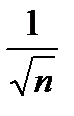
Следует также заметить, что известное нам выражение для оценки доли качественного признака через частоту переходит в формулу для оценки математического ожидания, если качественный признак описывается двузначной случайной величиной со значениями «0» и «1»

.

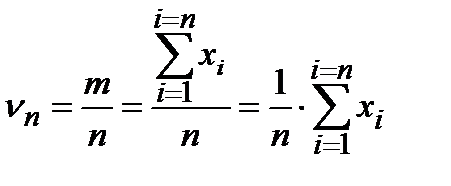Здесь m – количество появлений значения «1».

Так что вычисление среднего арифметического – это, по-прежнему, основной статистический приём.