Ошибка оценки – это отклонение полученной оценки от неизвестного значения оцениваемой вероятностной характеристики случайной величины.
Другое общеупотребительное название ошибки оценки – погрешность.
Оценка является случайной величиной. А раз так, можно говорить о наличии у такой случайной величины математического ожидания и дисперсии. Дисперсия и будет характеризовать ошибку оценки.
Оценивание должно производиться так, чтобы оценка имела как можно меньшую дисперсию. (Лучшим будет ружьё, которое обеспечивает наивысшую кучность стрельбы.)
В нашем курсе мы рассматриваем различные оценки, но наиболее подробно будем заниматься оценкой математического ожидания. Поэтому для неё мы получим необходимые выражения для вычисления ошибки. Но прежде договоримся об обозначениях.
Применительно к математическому ожиданию, рассеяние полученной оценки  относительно истинного значения M(X) описывается дисперсией оценки, которую можно обозначить как
относительно истинного значения M(X) описывается дисперсией оценки, которую можно обозначить как
 или
или  .
.
Чем больше объём выборки n, тем точнее оценка, т.е. тем меньше рассеяние возможных значений оценки, т.е. тем меньше дисперсия оценки:
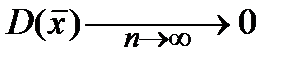 .
.
Для того, чтобы мера рассеяния оценки измерялась в тех же единицах измерения, что и сама оценка, из дисперсии оценки извлекают корень квадратный, и эта величина носит название среднеквадратической ошибки:
 =
= 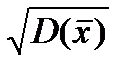 .
.
По смыслу, 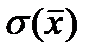 – это среднеквадратическое отклонение оценки математического ожидания от неизвестного значения оцениваемого математического ожидания.
– это среднеквадратическое отклонение оценки математического ожидания от неизвестного значения оцениваемого математического ожидания.
Полный ответ на вопрос о значении вероятностной характеристики случайной величины обязательно должен содержать указание величины возможной ошибки.
Поэтому надо уметь вычислять по выборочным данным не только саму оценку, но и оценивать ошибку этой полученной оценки.
Чтобы найти ошибку, надо уметь находить дисперсию оценки.
Но, как известно из теории вероятности, для получения точного значения дисперсии надо знать закон распределения или плотность распределения оценки, а они для неё неизвестны.
Поэтому самое большое, на что можно рассчитывать, это получить не саму дисперсию оценки, а её приблизительное значение, пользуясь выборкой. Обозначим оценку дисперсии математического ожидания так
 .
.
Поскольку эта оценка получена по выборке, она называется выборочная дисперсия оценки.
Для удобства из неё извлекают квадратный корень и обозначают, естественно, как 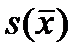 .
.
Название полученной величины – выборочная среднеквадратическая ошибка.
По смыслу, это – оценка среднеквадратического отклонения оценки.
Каковы формулы для вычисления этих оценок, узнаем чуть позже.
Как можно видеть, имеется определённая сложность в обозначениях: надо отличать саму величину от её оценки. Часто, чтобы не вводить новых букв, к обозначению величины добавляют «крышечку» наверху, и получается оценка этой величины.
Например:
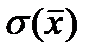 – среднеквадратическая ошибка,
– среднеквадратическая ошибка,
 – оценка среднеквадратической ошибки (хотя это то же самое, что
– оценка среднеквадратической ошибки (хотя это то же самое, что 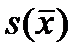 ).
).
 – дисперсия оценки математического ожидания,
– дисперсия оценки математического ожидания,
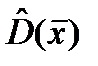 – оценка дисперсии оценки математического ожидания (хотя то же самое, что
– оценка дисперсии оценки математического ожидания (хотя то же самое, что  ).
).
Сведём все рассмотренные обозначения в сдвоенную таблицу: в левой половине – касающееся случайной величины X, в правой – касающееся оценки её математического ожидания  .
.
| Случайная величина X | Оценка мат. ожидания 
| |||
| Вероятност-ные характе-ристики | Оценки вероятностных характеристик | Вероятност-ные характе-ристики | Оценки вероятностных характеристик | |
| M(X) – мат. ожидание |  = = 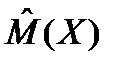 – оценка мат. ожидания – оценка мат. ожидания
| M(  ) = M(X) ) = M(X)
| = 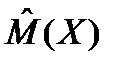
| |
D(X)=  – дисперсия (рассеяние) – дисперсия (рассеяние)
|  = =  – оценка дисперсии – оценка дисперсии
|  – дисперсия оценки мат. ожидания – дисперсия оценки мат. ожидания
|  = = 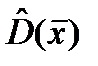
| |
| s – среднеквадр. отклонение | s =  – оценка среднеквадратического отклонения – оценка среднеквадратического отклонения
| 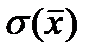 – ошибка оценки мат. ожидания – ошибка оценки мат. ожидания
| 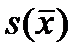 = = 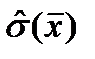 – оценка ошибки оценки мат. ожидания – оценка ошибки оценки мат. ожидания
|
В этой таблице выделим жирными границами ячейку с оценкой математического ожидания случайной величины  , которая нас больше всего интересует, а также ячейку с ошибкой этой оценки
, которая нас больше всего интересует, а также ячейку с ошибкой этой оценки 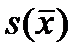 .
.
Дата добавления: 2021-01-26; просмотров: 918;











