ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ КАЧЕСТВЕННОГО ПРИЗНАКА

Качественный признак будет обсчитываться в домашнем задании.

Качественный признак с долей p в генеральной совокупности удобно описывать двузначной случайной величиной X с двумя возможными значениями: 0 и 1.

Пример. Корзина с чёрными и белыми шарами. Доля белых шаров – p. Желаемое значение качественного признака – белый цвет шара.

Вероятность того, что один наугад вынутый шар окажется белым: P(белый) = p.

Соответственно, вероятность достать чёрный шар: P(чёрный) = 1 – p.

Рассматриваем двузначную случайную величину X. Пусть белому цвету соответствует её значение 1, чёрному – 0.

Закон распределения для неё можно изобразить так (рисунок). Здесь случай, когда p ближе к 1, чем к 0.

Вычислим, зная закон распределения, математическое ожидание этой случайной величины.

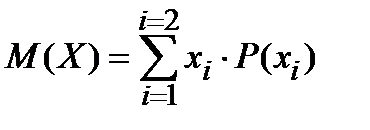= 0 × (1 – p) + 1 × p = p .

Нанесём это значение на рисунок.

Математическое ожидание указывает абсциссу центра тяжести, поэтому оно ближе к большему, более «тяжёлому» столбику.

0 1 x

(1 – p )

M(X)

p

p

Из полученного равенства следует, что доля качественного признака в генеральной совокупности p может вычисляться как математическое ожидание случайной величины с двумя возможными значениями 0 и 1.

Теперь вычислим дисперсию этой же двузначной случайной величины

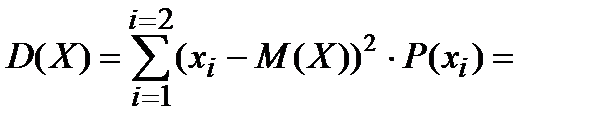(0 – p)² × (1 – p) + (1 – p)² × p =

= p² × (1 – p) + (1 – p)² × p = p × (1 – p) × (p + (1 – p) ) = p × (1 – p) .

Запомним итог. Он нам понадобится дальше.

А глядя на формулу, отметим себе, что дисперсия двузначной случайной величины зависит от исходной доли p.

Если доля p велика, т.е. близка к единице, то возможные значения из генеральной совокупности могут выглядеть, например, так:

1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 и т.д., т.е. преобладают единицы, а вся последовательность достаточно однообразна.

Если же p близка к 1/2, то значения из генеральной совокупности могут идти так:

0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0 и т.д., т.е. значения более разнообразны.

В этих примерах наблюдающееся разнообразие двух возможных значений можно выразить количественно. Это делается с помощью дисперсии.