Нормальное распределение
Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
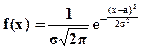 (5.10)
(5.10)
то говорят, что Х имеет нормальное распределение с параметрами а и 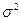 . Вероятностный смысл параметров:
. Вероятностный смысл параметров: 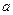 =М(X), а
=М(X), а 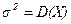 .Обозначение:
.Обозначение:
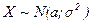
Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от 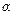 до
до 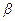 используется формула:
используется формула:
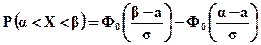 (5.11)
(5.11)
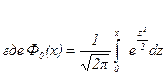 (интеграл Лапласа)
(интеграл Лапласа)
Формула (5.11) иногда в литературе называется интегральной теоремой Лапласа.
Функция 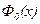 обладает свойствами:
обладает свойствами:
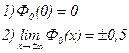
3) 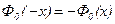 (см. таблицу приложения 2).
(см. таблицу приложения 2).
Функция 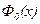 табулирована. В частности для симметричного относительно а промежутка
табулирована. В частности для симметричного относительно а промежутка 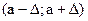 имеем:
имеем:
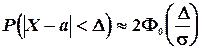 (5.12)
(5.12)
Формула (5.12) применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик
M(m) = np и 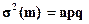 (5.13)
(5.13)
формула (5.12) примет вид :
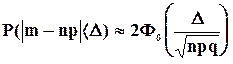 (5.14)
(5.14)
Формула (5.12) может быть применена и к относительной частоте 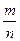 с числовыми характеристиками
с числовыми характеристиками 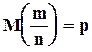 и
и 
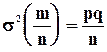
 (5.15)
(5.15)
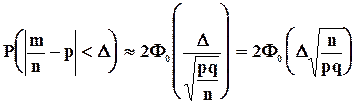 (5.16)
(5.16)
С вероятностью, очень близкой к единице (равной 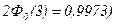 нормально распределенная случайная величина Х удовлетворяет неравенству:
нормально распределенная случайная величина Х удовлетворяет неравенству:
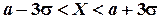 (5.17)
(5.17)
В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает 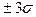 .
.
Локальная теорема Муавра-Лапласа. При р 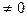 и p
и p 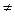 1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
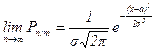 , где
, где 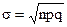 , a=nр
, a=nр
Тогда:
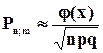 (5.18)
(5.18)
для достаточно больших n (здесь 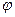 (х) - плотность вероятностей стандартной нормальной случайной величины
(х) - плотность вероятностей стандартной нормальной случайной величины 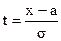 и
и 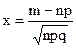 ).
).
Дата добавления: 2016-10-26; просмотров: 1774;











