Функция распределения и плотность распределения непрерывной случайной величины.

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна и имеет производную.

Как уже было показано в разделе 4 (формула 4.2), функцией распределения случайной величины Х называется функция F(X), выражающая вероятность выполнения условия :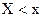

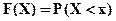(5.1)

Функция распределения обладает следующими свойствами:

1.Вероятность попадания случайной величины в промежуток от 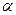до 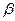равна приращению функции распределения на концах этого промежутка:

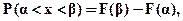(5.2),

так как вероятность любого отдельного значения случайной величины равна нулю, если функция распределения непрерывна при этом значении, т. е. :

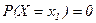, когда F(X) - непрерывна в точке =

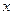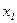
2.Функция распределения удовлетворяет условиям:

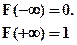( 5.3)

Плотностью распределения (дифференциальной функцией) непрерывной случайной величины называется функция

f(x) = 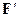(x). (5.4)

Плотность распределения любой случайной величины неотрицательна: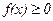

Несобственный интеграл от дифференциальной функции в пределах от - 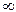до + 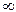равен 1:

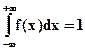(5.5)

График функции y = f(x) называется кривой распределения или графиком плотности распределения. Кривая y = f (x) располагается над осью абсцисс.

Вероятность попадания случайной величины в промежуток от 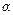до 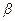может быть вычислена по формуле:

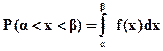(5.6)

Подинтегральное выражение f(x)dx называется элементом вероятности. Оно выражает вероятность попадания случайной точки в промежуток между точками х и 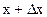, где 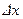бесконечно малая величина.

Функция распределения F(x) выражается через плотность f(x) формулой :

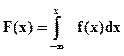(5.7)

Математическое ожидание непрерывной случайной величины Х вычисляется по формуле:

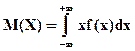(5.8),

дисперсия 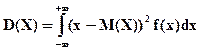(5.9)

<910 11 12 13 14 15 >

Дата добавления: 2016-10-26; просмотров: 2647;