Числовые характеристики вариационного ряда
Одной из основных числовых характеристик ряда распределения (вариационного ряда) является средняя арифметическая.
Существует две формулы расчета средней арифметической: простая и взвешенная.
Простую среднюю арифметическую обычно используют, когда данные наблюдения не сведены в вариационный ряд либо все частоты равны единице или одинаковы.
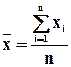 ; (6.8)
; (6.8)
где xi - i-е значение признака;
n - объем ряда (число наблюдений; число значений признака).
В том случае, если частоты отличны друг от друга, расчет производится по формуле средней арифметической взвешенной:
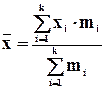 ; (6.9)
; (6.9)
где xi - i-е значение признака;
mi - частота i-го значения признака;
k - число значений признака (вариантов).
При расчете средней арифметической в качестве весов могут выступать и частости. Тогда формула расчета средней арифметической взвешенной примет следующий вид:
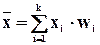 (6.10)
(6.10)
где xi - i-е значение признака;
wi - частость i-го значения признака;
k - число значений признака (вариантов).
Колеблемость изучаемого признака можно охарактеризовать с помощью различных показателей вариации. К числу основных показателей вариации относятся: дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Дисперсию можно рассчитать по простой и взвешенной формуле.
Простая имеет вид:
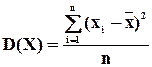 . (6.11)
. (6.11)
А взвешенная:
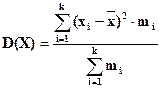 . (6.12)
. (6.12)
Среднее квадратическое отклонение рассчитывается по формуле:
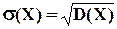 (6.13)
(6.13)
Коэффициент вариации рассчитывается по формуле:
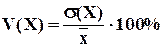 . (6.14)
. (6.14)
Дата добавления: 2016-10-26; просмотров: 7535;











