Понятие полной группы событий.

Если имеются события А_1, А₂, …, А_i …, А_N такие, что

1) они попарно не совместны, т.е.

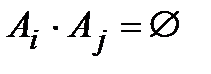при i ¹ j

2) их сумма исчерпывает достоверное событие (составляет достоверное событие), т.е.

A₁ + A₂ + … + A_i + … + A_N = W ,

Ω

A1

A2

A3

Ai

AN

то совокупность таких событий называются полной группой событий.

Вероятность суммы полной группы событий равна единице:

P(A₁ + A₂ + … + A_N) = P(W) = 1

Пример полной группы событий – совокупность всех элементарных исходов опыта.

Для вероятности суммы полной группы событий сокращённая запись такова:

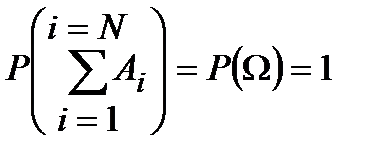
Для любознательных.

А что, если события A и B таковы, что они не обладают свойством несовместности, т.е. ?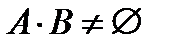

В этом случае вероятность их суммы вычисляется по более сложной формуле:

.

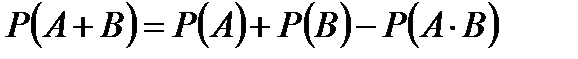7.8. ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
ПЛОТНОСТЬ ВЕРОЯТНОСТИ

Возможен другой способ определения вероятности: геометрический.

Вспомним доску Гальтона.

Шарики падают из воронки и попадают на горизонтальную ось x.

При падении они сталкиваются с препятствиями, поэтому заранее предсказать точку падения на оси невозможно.

Вся ось отождествляется с достоверным событием W. Т.е. вероятность того, что шарик попадёт на ось куда бы то ни было, равна единице. В воздухе он не зависнет.

Каждая точка оси – это элементарный исход, т.е. возможное место падения шарика.

Событие – это попадание шарика в пределы заданного отрезка на оси х.

х0

х0+Dх/2

х0–Dх/2

Dх

Вероятность элементарного исхода – это вероятность попадания шарика в определённую точку на оси.

При данной постановке опыта очевидно, что шарики падают в область непосредственно под воронкой чаще, а вдали от неё – реже.

Каковы отличия от классического определения вероятности?

1. Количество элементарных исходов бесконечно.

2. Вероятности элементарных исходов различны.

Теперь рассмотрим следующий любопытный вопрос.

А какова вероятность попадания в точку?

Ответ: бесконечно малая величина, потому что точка имеет бесконечно малую толщину. Т.е. почти ноль. Но всё же не ноль.

Вместе с тем, как было указано, вероятность попадания шарика в точку оси прямо под воронкой выше, чем вдали от неё.

Как учесть эти два обстоятельства и предложить способ определения вероятности?

Сделаем следующее.

1. На горизонтальной оси выберем точку x₀ и отложим в её окрестности отрезок длиной Dx.

2. Рассмотрим событие А, состоящее в том, что шарик попадёт в пределы этого отрезка. Вероятность такого события P(A) уже не будет бесконечно малой величиной. Это вероятность попадания в ящичек в опыте Гальтона.

3. Начнём уменьшать длину этого отрезка, постепенно стягивая его в точку x₀

Dx ® 0.

При этом начинает уменьшаться и вероятность попадания шарика в пределы отрезка

P(A) ® 0.

4. Рассмотрим отношение этих величин.

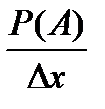
Оказывается, что при одновременном уменьшении и числителя, и знаменателя дробь будет стремиться к некоторой определённой величине

.

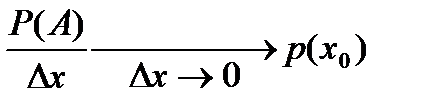Эта величина носит специальное название: плотность вероятности.

Плотность в физике – это масса на единицу объёма. А здесь у нас вероятность на единицу длины.

Плотность вероятности зависит от выбора точки x₀ и характеризует вероятность попадания шарика в окрестность точки x₀ .

Для её обозначения используется латинская буква p, но не большая, как для вероятности, а маленькая.