КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Мы помним, что вероятность – это численная мера возможности
Под словами «определение вероятности» мы будем понимать не формулировку, мол, что это такое, а способ установления этой численной меры.
Мы уже рассмотрели статистический способ определения вероятности, т.е. через частоту. Он прост и понятен.
Но определять вероятность, проводя многократные опыты, часто крайне затратно.
Поэтому рассмотрим другие подходы к определению вероятности.
Первым рассмотрим классическоеопределение вероятности.
Этот способ состоит из трёх положений.
1) Пространство элементарных исходов W состоит из N равновозможных элементарных исходов.
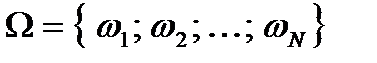 .
.
N – конечное число (это непременное условие!).
2) Вероятность любого i-ого элементарного исхода определяется просто как:
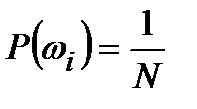 .
.
Ещё раз подчеркнём: исходы равновозможны, следовательно, равновероятны.
3) Вероятность любого события A определяется как
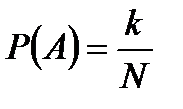 ,
,
где k – число элементарных исходов, из которых состоит событие А.
Чисто внешне последняя формула похожа на формулу для частоты, но в ней всё другое:
в числителе – не число выпадений события A в последовательности опытов, а число благоприятных исходов, возможных в условиях данного опыта,
в знаменателе – не число опытов, а общее число элементарных исходов.
При таком подходе для определения вероятности нет необходимости в проведении многочисленных опытов.
Достаточно 1) убедиться в равновозможности всех исходов, 2) убедиться в конечности их числа, 3) подсчитать число благоприятных исходов среди всех и 4) разделить на их общее число.
Так для ровной, непогнутой монеты можно сразу сказать, что вероятность выпадения орла равна 1/2.
А вероятность вытащить короля бубей из полной колоды равна 1/52.
7.7. СВОЙСТВА ВЕРОЯТНОСТИ.
ПОЛНАЯ ГРУППА СОБЫТИЙ
Свойства вероятности очень похожи на свойства частоты.
Свойство 1.
Для любого случайного события A
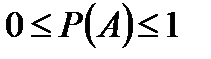 .
.
Свойство 2.
Вероятность невозможного события равна нулю, т.е.
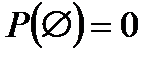 .
.
Свойство 3.
Вероятность достоверного события равна единице, т.е.
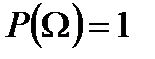 .
.
Свойство 4.
Если A и B – несовместные события, т.е. 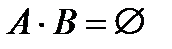 ,
,
то 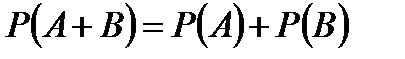 .
.
В этой последней записи между вероятностями стоит знак арифметического сложения, потому что вероятность это число. А внутри скобок – знак суммы событий. У этих знаков разные смыслы.
Несколько особняком стоит свойство 5.
Свойство 5.
Если A и B – независимые события, т.е. такие, что вероятность любого из них не зависит от того, произошло другое событие или нет,
то вероятность произведения независимых событий равна произведению вероятностей этих событий:
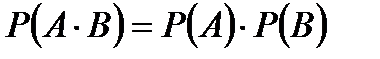 .
.
И 4-е, и 5-е свойства можно распространить на случай нескольких событий.
Рассмотрим 4-е свойство:
Если события А1, А2, …, Аn попарно несовместны, т.е.
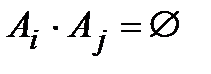 при
при 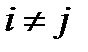 ,
,
то вероятность суммы несовместных событий равна сумме вероятностей этих событий:
P(A1 + A2 + … + Ai + … + An) = P(A1) + P(A2) + … + P(Ai) … + P(An).
Теперь подошло время познакомимся с одним математическим обозначением, которое оказывается удобным, когда в записи формулы возникает много слагаемых, похожих друг на друга.
Если посмотреть на формулу для вероятности суммы событий, то видно, что в ней складываются «А» с изменяющимися порядковыми номерами внизу:
A1 + A2 + … + Ai + … + An
Номера идут от 1 до n. Обобщённый промежуточный номер обозначен номером i.
Для более краткой записи такой длинной суммы рисуют большую греческую букву «сигма», означающую сумму, а после неё обобщённое промежуточное слагаемое с номером i. Сверху и снизу знака суммы пишут, в каких пределах изменяется этот номер i, т.е. от 1 до n.
A1 + A2 + … + Ai + … + An = 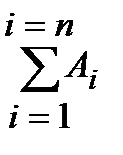
Очевидно, что запись суммы похожих слагаемых становится короче, хотя такая запись и непривычна. Но мы ею будем пользоваться в дальнейшем для краткости.
Рассмотрим, как с использованием этой записи будут выглядеть записанная нами прежде формула:
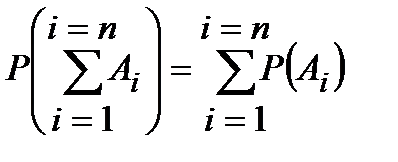
Дата добавления: 2021-01-26; просмотров: 602;











