ДЕЙСТВИЯ СО СЛУЧАЙНЫМИ СОБЫТИЯМИ
Событие С называется произведением событий А и В, если оно состоит из тех и только тех элементарных исходов, которые входят в А и В одновременно.
| A |
| Ω |
| B |
| C |
Обозначается как 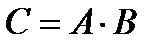 .
.
Широко используется также и другое обозначение: 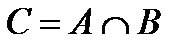 .
.
Оно заимствовано из теории множеств. Это вполне уместно, т.к. здесь событие рассматривается как множество исходов.
Однако для простоты мы будем использовать алгебраический значок умножить, а не значок объединения множеств. Не забывая, что смысл «умножить» другой.
| A |
| Ω |
| B |
| C |
Событие С называется суммой событий А и В, если оно состоит из тех элементарных исходов, которые входят либо в А, либо в В, либо в А и В одновременно.
Графический пример.
Обозначается как 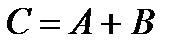 .
.
Широко используется также и другое обозначение: 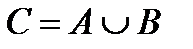 .
.
Но мы, по-прежнему, будем использовать знак плюс. И это не знак арифметического сложения!
Событие С называется разностью событий А и В, если оно состоит из тех и только тех элементарных исходов, которые одновременно входят в А и не входят в В.
| A |
| Ω |
| B |
| C |
Обозначается как 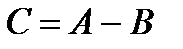 .
.
В теории множеств для разности используется и другое обозначение: С = A \ B .
Но мы будем использовать знак минус.
Этот знак минус не означает арифметическую разность, т.к. из 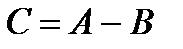 не следует, что
не следует, что 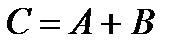 .
.
Знак плюс также не означает арифметическую сумму, т.е. из 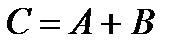 не следует, что
не следует, что 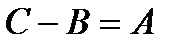 .
.
Знак умножить также не является арифметическим произведением, т.к. обратным к нему должно было бы быть действие деления, а оно для событий вообще не определено.
Исходя из определения разности событий А и В можно записать, что
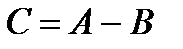 =
= 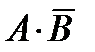
События А и В называются несовместными, если ни один из элементарных исходов, входящих в А, не входит в В, и наоборот.
Иными словами, наступление одного из них исключает наступление другого.
| A |
| Ω |
| B |
Изобразить несовместные события можно так
Математическая запись этого случая такая: 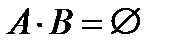 .
.
Дата добавления: 2021-01-26; просмотров: 705;











