ПЕРВЫЕ СТАТИСТИЧЕСКИЕ ОПЫТЫ И ХАРАКТЕРИСТИКИ: ВЕРОЯТНОСТЬ, ЧАСТОТА, НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Массовые случайные явления изучаются с помощью многократно повторяемых опытов. Возможный исход опыта со случайным явлением, называют случайным событием. Случайное событие – это событие, которое может произойти, а может не произойти в условиях данного опыта.
Случайное событие имеет большую или меньшую возможность осуществления.
Было бы крайне удобно, если бы степень этой возможности удалось выразить числом. Оно должно быть больше при большей возможности и меньше – при меньшей. Назовём такое число вероятностью.
Вероятность – это численная мера возможности данного случайного события.
Обычно вероятность некоторого случайного события А обозначается как Р(А).
P – от латинского слова probability.
Теперь надо придумать способ: как каждому случайному событию ставить в соответствие число, показывающее возможность его появления в опыте.
Рассмотрим простейший опыт со случайным явлением: подбрасывание монеты «орёл – решка». Опыт с двумя исходами.
Будем считать появление «решки» интересующим случайным событием А.
Пусть проведено n опытов.
Событие А имело место в m опытах.
Частота (или частость) случайного события А в n опытах, равна
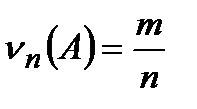 .
.
Эта греческая буква, n, читается как «ню» или «ни». По сути, это «эн» маленькое.
Частота – это число, и оно показывает, насколько возможно данное случайное событие в условиях данного опыта.
Частота обладает свойством устойчивости, т.е. при увеличении числа опытов она стремится к некоторому значению, которое называется вероятностью, т.е.
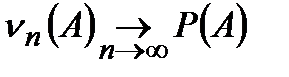
В случае с монетой частота стремится к значению 1/2.
Французский естествоиспытатель Жорж-Луи Бюффон в XVIII веке подбросил монету 4040 раз – и орёл выпал 2048 раз.
Способ определения вероятности через частоту носит название статистического определения вероятности. В дальнейшем будут рассмотрены также и другие способы: классическое и геометрическое определения вероятности.
Это пример того, как статистика питает теорию вероятности.
Рассмотрим ещё одно важное статистическое основание теории вероятностей.
Доска Гальтона.
Английский учёный Френсис Гальтон (1822-1911) – это статистик, антрополог, основатель евгеники, двоюродный брат Чарльза Дарвина.
Гальтон взял доску, вбил в неё стержни в несколько рядов и сверху через воронку сыпал шарики.
Шарики, падая, сталкивались со стержнями и отскакивали в различных направлениях. Внизу Гальтон расположил ящик с узкими отделениями одинаковой ширины и занялся подсчётом числа шариков, попадающих в различные отделения.
При большом числе шариков им было замечено следующее: заполнение отделений происходило так, что уровни в отделениях неизменно образовывали колоколообразную кривую (второй рисунок).
Математиками была найдена строгая формула для этой кривой. Мы с её математической записью познакомимся несколько позже. Сейчас же укажем, что в её состав входит такая функция переменной x:
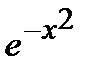 , где x – горизонтальная координата.
, где x – горизонтальная координата.
Называется эта колоколообразная кривая кривой нормального распределения.
Вблизи основания кривой можно указать интервал, куда возможность упасть шарику наибольшая, или, иными словами, куда падает основное количество шариков. Этот интервал мы рассмотрим в дальнейшем весьма подробно.
СВОЙСТВА ЧАСТОТЫ
Итак, мы с вами уже познакомились с таким понятием как частота.
Т.е если поставлено n опытов, в которых может наблюдаться случайное событие А, то частота этого явления будет равна
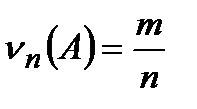 .
.
Свойство первое:
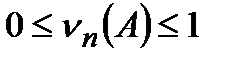 ,
,
т.е. частота – величина неотрицательная и не превосходящая единицы.
Свойство второе:
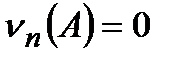 ,
,
т.е. частота равна нулю, если случайное событие А в n опытах не произошло ни разу.
Свойство третье:
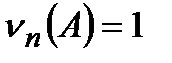 ,
,
т.е. частота равна единице, если случайное событие А наблюдалось во всех n опытах.
Свойство четвёртое.
Если случайные события А и В не встречаются одновременно, то можно рассмотреть событие С, состоящее в том, что в опыте появляется или А, или В.
С = «или А, или В»
Например, при бросании кубика А – выпадение 1 очка, В – выпадение 6 очков, С – выпадение одного из крайних значений.
Обозначим через 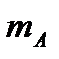 – число появления А;
– число появления А;
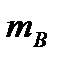 – число появлений В;
– число появлений В;
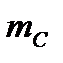 – число появлений С.
– число появлений С.
тогда
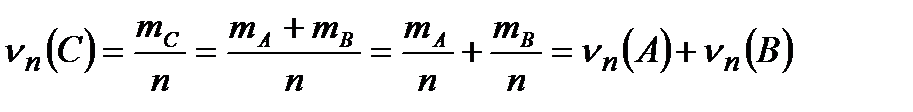 .
.
Дата добавления: 2021-01-26; просмотров: 700;











