Дифференциальное уравнение теплопроводности

Для вычисления температуры точек тела необходимо не только установить тепловой поток через заданное сечение, но и определить количество теплоты, поступающей в некоторый элементарный объем, а также уходящей из него.

Рассмотрим неравномерно нагретый стержень

Т

х

Согласно закону Фурье, тепловой поток в каждом сечении

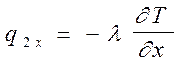
Приращение удельного теплового потока dq_2x на длине dx составит

.

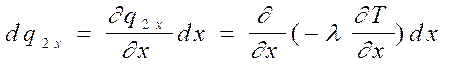За время dt в элементарном объеме Fdx накапливается количество теплоты

dQx = - dq_2x Fdt .

Знак минус означает, что через сечение I вошло больше теплоты, чем вышло через сечение II.

Однако через боковую поверхность стержня за время dt часть теплоты отдается в окружающее пространство

dQp = q_2p pdxdt,

где q_2p =a(Т-Тс) – удельный тепловой поток с боковой поверхности стержня с периметром р .

Суммарное количество теплоты, которое накапливается в элементарном объеме, составит

dQ= dQx - dQp

Теплота dQ повышает температуру элементарного объема массой rFdx на 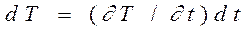в соответствии с уравнением

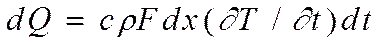
Делая соответствующие подстановки для dQ и произведя сокращения, получим дифференциальное уравнение теплопроводности для стержня

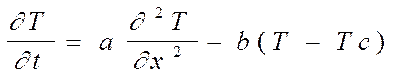
где a=l/cr – коэффициент температуропроводности, см²/с;

b=ap/(crF) – коэффициент температуроотдачи для стержня.

Для двухмерного случая дифференциальное уравнение теплопроводности примет вид

,

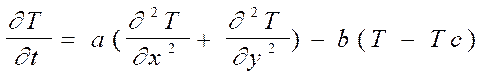где b=2a/(crd) – коэффициент температуроотдачи для пластины толщиной d .

Для трехмерного тела при отсутствии теплообмена с окружающей средой примет вид

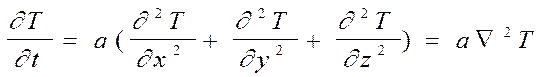
При выводе дифференциальных уравнений теплопроводности предполагалось, что теплофизические коэффициенты постоянны и не зависят от температуры. Учет их зависимости от температуры приводит к нелинейным дифференциальным уравнениям, что чрезвычайно усложняет получение решения аналитическими методами и делает неприемлемым принцип суперпозиции. В большинстве практических случаев точность решения оказывается достаточной, если выбирать средние значения теплофизических величин в исследуемом диапазоне температур.